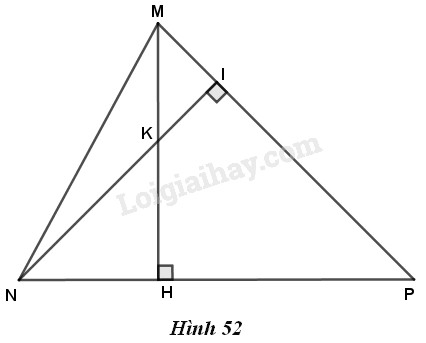
Bài 56 trang 98 Vở bài tập toán 7 tập 2Giải bài 56 trang 98 VBT toán 7 tập 2. Cho tam giác nhọn MNP. Hai đường cao MH, NI cắt nhau tại K Đề bài Cho tam giác nhọn MNP. Hai đường cao MH,NI cắt nhau tại K (h.52). a) Chứng minh PK⊥MN. b) Khi ^MPN=50∘. Hãy tính góc NKH.
Phương pháp giải - Xem chi tiết a) Chứng minh PK đi qua giao điểm của hai đường cao MH; NI. b) Chứng minh góc MPN bằng góc NHK. Lời giải chi tiết GT:ΔMNPnhọn,MH⊥NP,NI⊥MP,MH∩NI={K}KL:a)PK⊥MNb)^MPN=500.^NKH=? a) Do ba đường cao của một tam giác đồng quy tại một điểm nên đường cao thứ ba của tam giác đi qua giao điểm của hai đường cao còn lại. Vậy đường cao xuất phát từ P của tam giác MNP phải đi qua giao điểm của hai đường cao xuất phát từ M và N, hay PK⊥MN. b) Trong tam giác vuông MHP, ta có ^PMH+^MPH=90∘ (1) Trong tam giác vuông KIM, ta có ^KMI+^MKI=90∘ (2) Từ (1) và (2) suy ra ^MKI=^MPH, mà ^MKI=^NKH (hai góc đối đỉnh) nên ^MPN=^NKH. Khi ^MPN=50∘ thì ^NKH=50∘. HocTot.Nam.Name.Vn
|