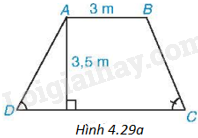
Giải bài 6 trang 87 vở thực hành Toán 9Mặt cắt ngang của một đập ngăn nước có dạng hình thang ABCD (H.4.29a). Chiều rộng của mặt trên AB của đập là 3m. Độ dốc của sườn AD, tức là (tan D = 1,25). Độ dốc của sườn BC, tức là (tan C = 1,5). Chiều cao của đập là 3,5m. Hãy tính chiều rộng CD của chân đập, chiều dài của các sườn AD và BC (làm tròn đến dm). Tổng hợp Đề thi vào 10 có đáp án và lời giải Toán - Văn - Anh Đề bài Mặt cắt ngang của một đập ngăn nước có dạng hình thang ABCD (H.4.29a). Chiều rộng của mặt trên AB của đập là 3m. Độ dốc của sườn AD, tức là \(\tan D = 1,25\). Độ dốc của sườn BC, tức là \(\tan C = 1,5\). Chiều cao của đập là 3,5m. Hãy tính chiều rộng CD của chân đập, chiều dài của các sườn AD và BC (làm tròn đến dm).
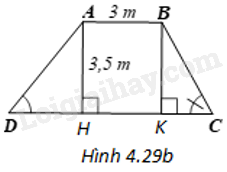
Phương pháp giải - Xem chi tiết + Kẻ các đường cao AH, BK của hình thang ABCD thì D, H, K, C nằm theo thứ tự đó trên đoạn DC. + Trong tam giác vuông AHD, ta có \(DH = \frac{{AH}}{{\tan D}}\), tính được DH. + Trong tam giác vuông BKC, ta có \(KC = \frac{{BK}}{{\tan C}}\), tính được KC. + Ta có: \(DC = DH + HK + KC\) + Áp dụng định lí Pythagore vào tam giác AHD vuông tại H tính được AD. + Áp dụng định lí Pythagore vào tam giác BKC vuông tại K tính được BC. Lời giải chi tiết (H.4.29b)
Kẻ các đường cao AH, BK của hình thang ABCD thì D, H, K, C nằm theo thứ tự đó trên đoạn DC. Trong tam giác vuông AHD, ta có \(DH = \frac{{AH}}{{\tan D}} = \frac{{3,5}}{{1,25}} = 2,8\) Trong tam giác vuông BKC, ta có \(KC = \frac{{BK}}{{\tan C}} = \frac{{3,5}}{{1,5}} \approx 2,3\) Ta có: \(DC = DH + HK + KC = 2,8 + 3 + 2,3 = 8,1\left( m \right)\) Trong tam giác AHD, ta có \(A{D^2} = A{H^2} + H{D^2} = {3,5^2} + {2,8^2}\), suy ra \(AD \approx 4,5m\). Trong tam giác vuông BKC, ta có \(B{C^2} = B{K^2} + K{C^2} = {3,5^2} + {2,3^2}\), suy ra \(BC \approx 4,2m\).
|