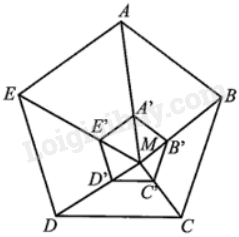
Giải bài 6 trang 107 sách bài tập toán 9 - Cánh diều tập 2Cho ngũ giác đều ABCDE và một điểm M nằm trong ngũ giác. Gọi A’, B’, C’, D’, E’ lần lượt là các điểm nằm trên các đoạn thẳng MA, MB, MC, MD, ME sao cho (frac{{MA'}}{{MA}} = frac{{MB'}}{{MB}} = frac{1}{3},frac{{CC'}}{{MC}} = frac{{DD'}}{{MD}} = frac{2}{3},frac{{ME'}}{{E'E}} = frac{1}{2}). Chứng minh ngũ giác A’B’C’D’E’ là ngũ giác đều. Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn - Cánh diều Toán - Văn - Anh - KHTN - Lịch sử và Địa lí Đề bài Cho ngũ giác đều ABCDE và một điểm M nằm trong ngũ giác. Gọi A’, B’, C’, D’, E’ lần lượt là các điểm nằm trên các đoạn thẳng MA, MB, MC, MD, ME sao cho \(\frac{{MA'}}{{MA}} = \frac{{MB'}}{{MB}} = \frac{1}{3},\frac{{CC'}}{{MC}} = \frac{{DD'}}{{MD}} = \frac{2}{3},\frac{{ME'}}{{E'E}} = \frac{1}{2}\). Chứng minh ngũ giác A’B’C’D’E’ là ngũ giác đều. Phương pháp giải - Xem chi tiết Dựa vào dữ kiện đề bài và định lí Thalès đảo để chứng minh các góc của ngũ giác A’B’C’D’E’ bằng nhau. Chứng minh A’B’ = B’C’ = C’D’ = D’E’ = E’A’ rồi suy ra ngũ giác A’B’C’D’E’ là ngũ giác đều. Lời giải chi tiết
Từ \(\frac{{MA'}}{{MA}} = \frac{{MB'}}{{MB}} = \frac{1}{3},\frac{{CC'}}{{MC}} = \frac{{DD'}}{{MD}} = \frac{2}{3},\frac{{ME'}}{{E'E}} = \frac{1}{2}\) suy ra: \(\frac{{MA'}}{{MA}} = \frac{{MB'}}{{MB}} = \frac{{MC'}}{{MC}} = \frac{{MD'}}{{MD}} = \frac{{ME'}}{{ME}} = \frac{1}{3}.\) (1) Do đó: A’B’ // AB, B’C’ // BC, C’D’ // CD, D’E’ // DE, E’A’ // EA (định lí Thalès đảo). Do A’B’ // AB nên \(\widehat {MA'B'} = \widehat {MAB}\) (đồng vị); Do E’A’ // EA nên \(\widehat {MA'E'} = \widehat {MAE}\)(đồng vị); Suy ra \(\widehat {MA'B'} + \widehat {MA'E'} = \widehat {MAB} + \widehat {MAE}\) hay \(\widehat {B'A'E'} = \widehat {BAE}\). Chứng minh tương tự, ta được các góc A’, B’, C’, D’, E’ của ngũ giác A’B’C’D’E’ tương ứng bằng các góc A, B, C, D, E của ngũ giác đều ABCDE. Mà ABCDE là ngũ giác đều nên góc A, B, C, D, E của ngũ giác bằng nhau. Do đó các góc của ngũ giác A’B’C’D’E’ bằng nhau. (2) Mặt khác, từ (1) ta cũng chứng minh được: \(A'B' = \frac{{AB}}{3};B'C' = \frac{{BC}}{3};C'D' = \frac{{CD}}{3};\) \(D'E' = \frac{{DE}}{3};E'A' = \frac{{EA}}{3}\). Mà ABCDE là ngũ giác đều nên AB = BC = CD = DE = EA. Do đó: A’B’ = B’C’ = C’D’ = D’E’ = E’A’. (3) Từ (2) và (3) suy ra ngũ giác A’B’C’D’E’ là ngũ giác đều.
|