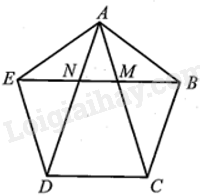
Giải bài 7 trang 107 sách bài tập toán 9 - Cánh diều tập 2

Đề bài

Cho ngũ giác đều ABCDE, đoạn BE cắt các đoạn AC và AD lần lượt tại M và N. Chứng minh rằng:

a) Các tam giác AEN và CMB là các tam giác cân;

b) AN là phân giác của góc EAM;

c) AB.BC = BM.AC.

Lời giải chi tiết

a) Ngũ giác ABCDE là ngũ giác đều nên AB = BC = CD = DE = EA và 

\(\widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEA} = \widehat {EAB}\).

Ta cũng có tổng 5 góc của ngũ giác đều ABCDE bằng tổng các góc của ba tam giác ABC, ACD, ADE, tức là bằng 3.180° = 540°.

Do đó, \(\widehat {ABC} = \widehat {BCD} = \widehat {CDE} = \widehat {DEA} = \widehat {EAB} = \frac{{{{540}^o}}}{5} = {108^o}\).

Xét ∆AEB cân tại A (do AB = AE) ta có:

\(\widehat {ABE} = \widehat {AEB} = \frac{{{{180}^o} - \widehat {EAB}}}{2} = \frac{{{{180}^o} - {{108}^o}}}{2} = {36^o}\)  hay \(\widehat {ABM} = \widehat {AEN} = {36^o}\).

Tương tự, đối với ∆EAD cân tại E ta có: \(\widehat {EAD} = \widehat {EDA} = {36^o}\) hay \(\widehat {EAN} = {36^o}\).

Do đó ta có \(\widehat {EAN} = \widehat {NEA} = {36^o}\) .Suy ra ∆AEN cân tại N.

Tương tự, ta chứng minh được ∆MAB cân tại M (do \(\widehat {MAB} = \widehat {MBA} = {36^o}\))

Suy ra \(\widehat {AMB} = {180^o} - 2\widehat {MAB} = {180^o} - {2.36^o} = {108^o}\).

Mặt khác: \(\widehat {CMB} = {180^o} - \widehat {AMB} = {180^o} - {108^o} = {72^o}\)

\(\widehat {MBC} = \widehat {ABC} - \widehat {ABM} = {180^o} - {36^o} = {72^o}\)

Suy ra tam giác CMB cân tại C.

b) Ta có \(\widehat {EAB} = \widehat {EAN} + \widehat {NAM} + \widehat {MAB}\)

Suy ra \(\widehat {NAM} = \widehat {EAB} - \widehat {EAN} - \widehat {MAB} = {180^o} - {36^o} - {36^o} = {36^o}\).

Do đó \(\widehat {EAN} = \widehat {NAM} = {36^o}\).

Vì vậy AN là phân giác của góc EAM.

c) Xét ∆MAB và ∆BAC có:

\(\widehat {AMB} = \widehat {ABC} = {108^o}\) và \(\widehat {BAC}\) là góc chung.

Do đó ∆MAB ᔕ ∆BAC (g.g), suy ra \(\frac{{AB}}{{AC}} = \frac{{BM}}{{CB}}\) hay AB.BC = BM.AC.