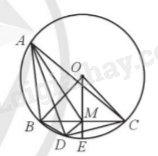
Giải bài 54 trang 124 sách bài tập toán 9 - Cánh diều tập 1

Đề bài

Cho đường tròn (O; R) và ba điểm A, B, C nằm trên đường tròn với AB < AC. Gọi M là trung điểm của đoạn thẳng BC. Trên cung BC không chứa điểm A, lấy điểm D sao cho $\widehat {BAD} = \widehat {CAM}$.

a) Chứng minh $\widehat {ADB} = \widehat {CDM}$.

b) Gọi E là giao điểm của tia OM và cung BC. Tính diện tích hình quạt tròn giới hạn bởi các bán kính OE, OC và cung nhỏ CE theo R, biết $BC = R\sqrt 2$.

Lời giải chi tiết

a) Ta có $\widehat {BAD} + \widehat {DAM} = \widehat {BAM},\widehat {DAM} + \widehat {CAM} = \widehat {DAC}$, mà $\widehat {BAD} = \widehat {CAM}$suy ra $\widehat {BAM} = \widehat {DAC}$.

Ta lại có $\widehat {ABM} = \widehat {ADC}$ (2 góc nội tiếp chắn cung AC của (O))

Xét tam giác ABM và tam giác ADC có:

$\widehat {ABM} = \widehat {ADC}$, $\widehat {BAM} = \widehat {DAC}$

Suy ra $\Delta ABM\backsim \Delta ADC$(g.g), do đó $\frac{{AB}}{{AD}} = \frac{{BM}}{{CD}} = \frac{{CM}}{{CD}}$.

Xét tam giác ABD và tam giác CMD có:

$\widehat {BAD} = \widehat {MCD}$ (góc nội tiếp cùng chắn cung BD của (O))

$\frac{{AB}}{{AD}} = \frac{{CM}}{{CD}}$

Suy ra $\Delta ABD\backsim \Delta CMD$(c.g.c), do đó $\widehat {ADB} = \widehat {CDM}$.

b) Xét tam giác OBM và tam giác OCM có:

OM chung

$OB = OC$(bằng bán kính (O))

$MB = MC$(M là trung điểm của BC)

Suy ra $\Delta OBM = \Delta OCM$(c.c.c), do đó $CM = \frac{{BC}}{2} = \frac{{R\sqrt 2 }}{2}$ và $\widehat {OMB} = \widehat {OMC}$

Mà $\widehat {OMB} + \widehat {OMC} = 180^\circ$, suy ra $\widehat {OMB} = \widehat {OMC} = \frac{{180^\circ }}{2} = 90^\circ$

Áp dụng định lý Pythagore trong tam giác vuông OCM có:

$OM = \sqrt {O{C^2} - C{M^2}}  = \sqrt {{R^2} - {{\left( {\frac{{R\sqrt 2 }}{2}} \right)}^2}}  = \frac{{R\sqrt 2 }}{2}$

Ta thấy $OM = CM\left( { = \frac{{R\sqrt 2 }}{2}} \right)$ nên tam giác OCM vuông cân tại M, suy ra $\widehat {COE} = 45^\circ$.

Diện tích hình quạt tròn giới hạn bởi các bán kính OE, OC và cung nhỏ CE là:

$S = \frac{{\pi {R^2}.45}}{{360}} = \frac{{\pi {R^2}}}{8}$ (đvdt).