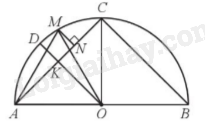
Giải bài 55 trang 124 sách bài tập toán 9 - Cánh diều tập 1Cho nửa đường tròn tâm O đường kính AB. Gọi C, D lần lượt là điểm chính giữa của cung AB, AC. a) Chứng minh ^BAC=^COD=^ABC=^ACO. b) Lấy điểm M thuộc cung CD. Chứng minh AM>CMvà ^COM=2^CAM. c) Khi M di chuyển trên cung nhỏ AC, tìm vị trí của điểm M để diện tích của tam giác MAC lớn nhất. Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn - Cánh diều Toán - Văn - Anh - KHTN - Lịch sử và Địa lí Đề bài Cho nửa đường tròn tâm O đường kính AB. Gọi C, D lần lượt là điểm chính giữa của cung AB, AC. a) Chứng minh ^BAC=^COD=^ABC=^ACO. b) Lấy điểm M thuộc cung CD. Chứng minh AM>CMvà ^COM=2^CAM. c) Khi M di chuyển trên cung nhỏ AC, tìm vị trí của điểm M để diện tích của tam giác MAC lớn nhất. Phương pháp giải - Xem chi tiết a) Bước 1: Tính số đo các cung CB, CA, CD, AD và từ đó tính được số đo các góc ABC, CAB, COD. Bước 2: Tính góc ACO (tổng 3 góc trong tam giác ACO). b) Bước 1: So sánh số đo cung AM và CM, từ đó suy ra ^ACM>^CAM. Bước 2: Dựa vào mỗi quan hệ giữ góc và cạnh đối diện trong tam giác ACM để so sánh AM, CM. c) Biểu diễn diện tích tam giác MAC: S=12AC.MN Ta dự đoán diện tích tam giác MAC khi M là điểm chính giữa của cung AC nên ta chứng minh MN≤DK. Lời giải chi tiết
Gọi K là giao điểm của AC và OD, kẻ MN vuông góc với AC tại N. a) Vì C điểm chính giữa của cung AB nên sđ⌢CB=sđ⌢CA=12sđ⌢AB=12.180∘=90∘ (do AB là cung chắn nửa đường tròn nên có số đo là 180⁰), Suy ra ^BAC=^ABC=90∘2=45∘(do ^BACvà ^ABClà các góc nội chắn các cung bằng nhau) (1) và ^COA=90∘(góc ở tâm chắn cung AC). Do D là điểm chính giữa của cung AC nên sđ⌢AD=sđ⌢DC=12sđ⌢AC=12.90∘=45∘ Suy ra ^COD=45∘ (do ^COD là góc ở tâm chắc cung DC)(2) Xét tam giác ABC có: ^ACO=180∘−^CAO−^COA=180∘−45∘−90∘=45∘ (3) Từ (1), (2), (3) suy ra ^BAC=^COD=^ABC=^ACO(=45∘). b) Do M thuộc cung nhỏ DC và sđ⌢AD=sđ⌢DC=45∘, mà sđ⌢AM=sđ⌢AD+sđ⌢DM=45∘+sđ⌢DM Nên sđ⌢AM>45∘ và sđ⌢CM<45∘, do đó sđ⌢AM>sđ⌢CM hay ^ACM>^CAM Xét tam giác ACM có ^ACM>^CAM nên AM>CM. Xét (O) có: ^CAM là góc nội tiếp chắn cung CM nên ^CAM=12sđ⌢CM; ^COM là góc ở tâm chắn cung CM nên ^COM=sđ⌢CM. Do đó ^COM=2^CAM. c) Diện tích tam giác MAC là S=12AC.MN. Mà AC cố định nên S lớn nhất khi MN lớn nhất. Do sđ⌢AD=sđ⌢DC nên ^COD=^AOD ( do đây là 2 góc ở tâm chắn 2 cung bằng nhau của (O)) nên OD (hay OK) là tia phân giác của góc COA. Mặt khác AO=CO (cũng bằng bán kính (O)) nên tam giác ACO cân tại O, do đó đường phân giác OK đồng thời là đường cao, hay OK⊥AC. Ta lại có MN+OK≤OMvà OM=OD=DK+OK nên MN≤DK. Do DK không đổi nên MN lớn nhất khi MN=DK hay M là điểm chính giữa cung AC. Vậy diện tích ΔMAClớn nhất bằng 12AC.DK khi M là điểm chính giữa cung nhỏ AC.
|