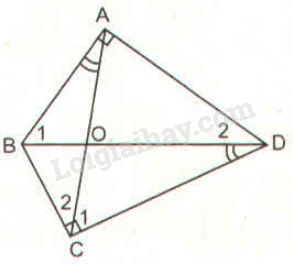
Bài 52 trang 97 SBT toán 8 tập 2

Đề bài

Tứ giác $ABCD$ có hai góc vuông tại đỉnh $A$ và $C,$ hai đường chéo $AC$ và $BD$ cắt nhau tại $O,$ $\widehat {BAO} = \widehat {BDC}$ (h.37)

Chứng minh:

a) $∆ ABO$ đồng dạng $∆ DCO$.

b) $∆ BCO$ đồng dạng $∆ ADO$.

Lời giải chi tiết

a) $\widehat {BAO} = \widehat {BDC}$  (gt) hay $\widehat {BAO} = \widehat {ODC}$

Xét $∆ABO$ và $∆ DCO$ có:

+) $\widehat {BAO} = \widehat {ODC}$ (chứng minh trên)

+)  $\widehat {AOB} = \widehat {DOC}$  (đối đỉnh)

$\Rightarrow  ∆ ABO$ đồng dạng $∆ DCO$ (g.g)

b) Vì $∆ ABO$ đồng dạng $∆ DCO$ nên ${\widehat B_1} = {\widehat C_1}$    (1)

Mà ${\widehat C_1} + {\widehat C_2} = \widehat {BCD} = 90^\circ$  (2)

Xét tam giác $ABD$ có $\widehat A = 90^\circ$ nên ${\widehat B_1} + {\widehat D_2} = 90^\circ$             (3)

Từ (1), (2) và (3) suy ra: ${\widehat C_2} = {\widehat D_2}$

Xét $∆ BCO$ và $∆ ADO$ có:

${\widehat C_2} = {\widehat D_2}$ (chứng minh trên )

$\widehat {BOC} = \widehat {AOD}$ (đối đỉnh)

$\Rightarrow ∆ BCO$ đồng dạng $∆ ADO$ (g.g).

HocTot.Nam.Name.Vn