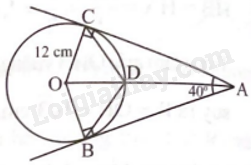
Giải bài 5 trang 89 sách bài tập toán 9 - Chân trời sáng tạo tập 1Từ điểm A nằm ngoài đường tròn (O; 12 cm) vẽ hai tiếp tuyến của (O) tại B, C. Đoạn thẳng OA cắt (O) tại D. Cho biết (widehat {BAC} = {40^o}). Tính: a) Số đo (widehat {OCD}). b) Độ dài các đoạn thẳng AC, AB, AO. (Làm tròn kết quả đến hàng đơn vị của mét) Tổng hợp Đề thi vào 10 có đáp án và lời giải Toán - Văn - Anh Đề bài Từ điểm A nằm ngoài đường tròn (O; 12 cm) vẽ hai tiếp tuyến của (O) tại B, C. Đoạn thẳng OA cắt (O) tại D. Cho biết \(\widehat {BAC} = {40^o}\). Tính: a) Số đo \(\widehat {OCD}\). b) Độ dài các đoạn thẳng AC, AB, AO. (Làm tròn kết quả đến hàng đơn vị của mét) Phương pháp giải - Xem chi tiết Dựa vào: Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến. Vận dụng tỉ số lượng giác của góc nhọn và hệ thức giữa cạnh và góc giúp giải tam giác vuông thuận lợi và nhanh chóng. Lời giải chi tiết
a) Ta có AO là tia phân giác của \(\widehat {BAC}\), suy ra \(\widehat {OAC} = \frac{{\widehat {BAC}}}{2} = {20^o}\). Tam giác OAC vuông tại C, suy ra \(\widehat {AOC} = {90^o} - \widehat {OAC} = {70^o}\) hay \(\widehat {DOC} = {70^o}\). Trong tam giác ODC cân tại O, ta có: \(\widehat {ODC} = \frac{{{{180}^o} - \widehat {COD}}}{2} = \frac{{{{180}^o} - {{70}^o}}}{2} = {55^o}\). b) AB = AC = OC. tan \(\widehat {AOC}\) = 12.tan 70o \( \approx \)33 (cm). OA = \(\frac{{OC}}{{\sin \widehat {OAC}}} = \frac{{12}}{{\sin {{20}^o}}} \approx 35(cm)\).
>> Học trực tuyến lớp 9 và Lộ trình UP10 trên Tuyensinh247.com Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Lộ trình học tập 3 giai đoạn: Học nền tảng lớp 9, Ôn thi vào lớp 10, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.
|