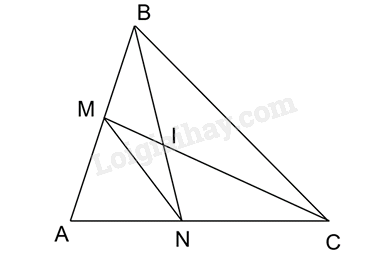
Giải bài 5 trang 88 vở thực hành Toán 8 tập 2Cho góc BAC và các điểm M, N lần lượt trên các đoạn thẳng AB, AC sao cho \(\widehat{ABN}=\widehat{ACM}\) Đề bài Cho góc BAC và các điểm M, N lần lượt trên các đoạn thẳng AB, AC sao cho \(\widehat{ABN}=\widehat{ACM}\) a) Chứng minh rằng ΔABN ∽ ΔACM. b) Gọi I là giao điểm của BN và CM. Chứng minh rằng IB.IN = IC.IM. Phương pháp giải - Xem chi tiết a) Chứng minh: tam giác ABN và tam giác ACM có góc A chung, \(\widehat{ABN}=\widehat{ACM}\) => ΔABN ∽ ΔACM b) Chứng minh: ΔIBM ∽ ΔICN (g.g) nên suy ra các tỉ số đồng dạng Lời giải chi tiết
a) Hai tam giác ABN và ACM có: $\widehat{ABN}=\widehat{ACM}$ (theo giả thiết), $\widehat{A}$ chung. b) Hai tam giác IBM và ICN có: $\widehat{IBM}=\widehat{ABN}=\widehat{ACM}=\widehat{ICN}$ (theo giả thiết), $\widehat{BIM}=\widehat{CIN}$(hai góc đối đỉnh). Vậy $\Delta IBM\backsim \Delta ICN(g.g)$. Suy ra $\frac{IB}{IC}=\frac{IM}{IN}$, hay IB.IN = IC.IM.  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
