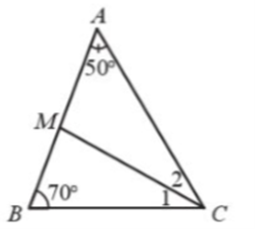
Giải Bài 5 trang 68 sách bài tập toán 7 - Cánh diều

Đề bài

Cho tam giác ABC có  Tia phân giác của góc C cắt cạnh AB tại M. Tính số đo của $\widehat {AMC}$ và $\widehat {BMC}$

Lời giải chi tiết

 

Xét ∆ABC có: $\widehat {{A^{}}} + \widehat B + \widehat C = {180^o}$ (định lí tổng ba góc của một tam giác).

Suy ra $\widehat {ACB} = {180^o} - \widehat {{A^{}}} - \widehat B = {180^o} - {50^o} - {70^o} = {60^o}$

Vì tia CM là tia phân giác của nên ta có:

$\widehat {{C_1}} = \widehat {{C_2}} = \frac{{\widehat C}}{2} = \frac{{{{60}^o}}}{2} = {30^o}$

Xét ∆AMC có: $\widehat {AMC} + \widehat {{C_2}} + \widehat {{A^{}}} = {180^o}$ (tổng ba góc của một tam giác).

Suy ra $\widehat {AMC} = {180^o} - \widehat {{C_2}} - \widehat {{A^{}}} = {180^o} - {30^o} - {50^o} = {100^o}$

 Xét ∆BMC có: $\widehat {BMC} + \widehat {{C_1}} + \widehat B = {180^o}$ (tổng ba góc của một tam giác).

Suy ra $\widehat {BMC} = {180^o} - \widehat {{C_1}} - \widehat B = {180^o} - {30^o} - {70^o} = {80^o}$

 Vậy $\widehat {AMC} = {100^o};\widehat {BMC} = {80^o}$