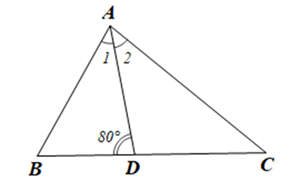
Giải Bài 9 trang 69 sách bài tập toán 7 - Cánh diềuCho tam giác ABC, tia phân giác của \(\widehat {BAC}\) cắt cạnh BC tại D. Tính số đo mỗi góc của tam giác ABC, biết \(\widehat {A{\rm{D}}B} = {80^o}\) và \(\widehat B = 1,5\widehat C\). Đề bài Cho tam giác ABC, tia phân giác của \(\widehat {BAC}\) cắt cạnh BC tại D. Tính số đo mỗi góc của tam giác ABC, biết \(\widehat {A{\rm{D}}B} = {80^o}\) và \(\widehat B = 1,5\widehat C\). Phương pháp giải - Xem chi tiết Sử dụng tổng ba góc của một tam giác bằng \({180^o}\) và tia phân giác của một góc để tìm số đo mỗi góc của tam giác ABC Lời giải chi tiết •Xét ∆ABD có: \({\hat A_1} + \hat B + \widehat {ADB} = 180^\circ \) (tổng ba góc của một tam giác) Suy ra \({\hat A_1} + \hat B = 180^\circ - \widehat {ADB} = 180^\circ - 80^\circ = 100^\circ \) Khi đó \({\hat A_1} = 100^\circ - \hat B\) Lại có \(\hat B = 1,5\hat C\) Suy ra \({\hat A_1} = 100^\circ - 1,5\hat C\)(1) •Vì \(\widehat {ADB}\) là góc ngoài của tam giác ACD tại đỉnh D nên \(\widehat {ADB} = \hat C + {\hat A_2}\) Suy ra \({\hat A_2} = \widehat {ADB} - \hat C = {80^o} - \hat C\)(2) • Ta có AD là tia phân giác của góc BAC nên \({\hat A_1} = {\hat A_2}\) (3) Từ (1),(2),(3) ta có: \(100^\circ - 1,5\hat C = 80^\circ - \hat C\) Hay \(1,5\hat C - \hat C = 100^\circ - 80^\circ \) Suy ra \(\hat C = 40^\circ \). Do đó \(\hat B = 1,5\hat C = 1,5.40^\circ = 60^\circ \) Xét ∆ABC có: \(\widehat {BAC} + \widehat B + \widehat C = {180^o}\) (tổng ba góc của một tam giác). Do đó \(\widehat {BAC} = 180^\circ - \hat C - \hat B = 180^\circ - 40^\circ - 60^\circ = 80^\circ \) Vậy \(\hat C = 40^\circ ,\hat B = 60^\circ ,\widehat {BAC} = 80^\circ .\)
|