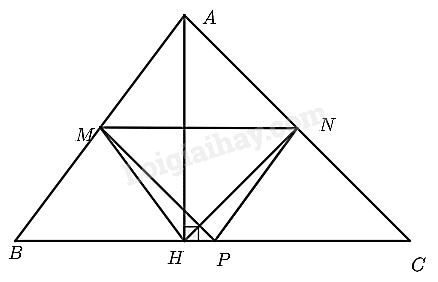
Giải bài 5 trang 54 SGK Toán 8 tập 2– Chân trời sáng tạoCho tam giác Tổng hợp đề thi học kì 2 lớp 8 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Khoa học tự nhiên Đề bài Cho tam giác \(ABC\) nhọn. Gọi \(M,N,P\) lần lượt là trung điểm của \(AB;AC;BC\). Kẻ đường cao \(AH\). Chứng minh rằng tứ giác \(MNPH\) là hình thang cân. Video hướng dẫn giải Phương pháp giải - Xem chi tiết - Đường trung bình của tam giác là đoạn thẳng nối hai trung điểm của tam giác. - Đường trung bình của tam giác song song với cạnh thứ ba và bằng nửa cạnh ấy. - Để chứng minh hình thang cân ta sẽ chứng minh hình thang có hai đường chéo bằng nhau hoặc hai góc kề một đáy bằng nhau. - Trong tam giác vuông, đường trung tuyến ứng với cạnh huyền thì bằng nửa cạnh huyền. Lời giải chi tiết
- Vì \(M\) là trung điểm của \(AB;N\) là trung điểm của \(AC\) nên \(MN\) là đường trung bình của tam giác \(ABC\). Do đó, \(MN//BC\) (tính chất đường trung bình). \( \Rightarrow MN//HP\left( {H;P \in BC} \right)\) Xét tứ giác \(MNPH\) có: \(MN//HP \Rightarrow \) tứ giác \(MNPH\) là hình thang. - Vì \(M\) là trung điểm của \(AB;P\) là trung điểm của \(AC\) nên \(MP\) là đường trung bình của tam giác \(ABC\). Do đó, \(MP = \frac{1}{2}AC\) (tính chất đường trung bình) (1). - Xét tam giác \(AHC\) vuông tại \(H\) có: \(N\)là trung điểm của \(AC\) nên \(HN = \frac{1}{2}AC\) (tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông) (2). Từ (1) và (2) suy ra \(MP = HN\). Xét hình thang \(MNPH\) có: \(MP = HN\) (chứng minh trên). Do đó, hình thang \(MNPH\) là hình thang cân (dấu hiệu nhận biết hình thang cân).  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K10 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
