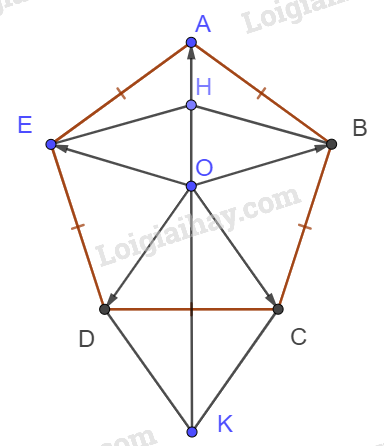
Giải bài 5 trang 103 sách bài tập toán 10 - Chân trời sáng tạoCho hình ngũ giác đều ABCDE có tâm O. Chứng minh rằng: Đề bài Cho hình ngũ giác đều ABCDE có tâm O. Chứng minh rằng: →OA+→OB+→OC+→OD+→OE=→0 Lời giải chi tiết Không mất tính tổng quát giả sử OA=OB=OC=OD=OE=1 Ta có: ^AOB=^BOC=^COD=^DOE=^EOA=360∘:5=72∘ + Dựng hình bình hành OEHB. Vì OE=OB nên OEHB là hình thoi, suy ra H thuộc tia phân giác của ^EOBhay H thuộc OA. ⇒→OA+(→OB+→OE)=→OA+→OH=→OM với M thuộc OA sao cho OM = OH +OA. + Tính OM: Xét tam giác OHE, ta có: ^HOE=72;OE=HE=1 ⇒^OHE=72o⇒^OEH=180∘−72o−72o=36∘ Áp dụng định lí cosin: OH2=OE2+EH2−2.OE.OH.cosE ⇔OH2=1+1−2.cos36∘≈0,382⇒OH=0,618⇒OM=OH+OA=0,618+1=1,618 + Dựng hình bình hành OCKD, ta có: →OC+→OD=→OK Vì OC=OD nên OCKD là hình thoi => OK là tia phân giác của ^COD ⇒^COK=12^COD=12.72o=36o ⇒^KOA=^KOC+^COB+^BOA=36∘+72∘+72∘=180∘ Hay K, O, A thẳng hàng, do đó K, O, M thẳng hàng (do M thuộc OA). +Tính OK: Xét tam giác OCK, ta có: OC=CK=1;^COK=36o⇒^CKO=36o⇒^OCK=180o−36o−36o=108o⇒OK2=OC2+CK2−2.OC.CK.cos^OCK⇔OK2=1+1−2.cos108o≈2,618⇒OK=1,618=OM Vậy O là trung điểm KM hay →OK+→OM=→0 ⇒→OA+→OB+→OC+→OD+→OE=(→OA+→OB+→OE)+(→OC+→OD)=→OM+→OK=→0(dpcm)
|