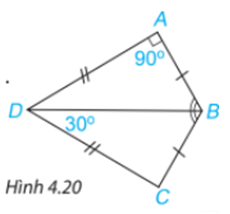
Giải bài 4.6 trang 67 SGK Toán 7 tập 1 - Kết nối tri thức

Đề bài

Cho Hình 4.20, biết $AB = CB, AD = CD,\widehat{DAB} = {90^\circ },\widehat{BDC} = {30^\circ }$

a) Chứng minh rằng $\Delta ABD = \Delta CBD$.

b) Tính $\widehat {ABC}$.

Lời giải chi tiết

a)      Xét $\Delta ABD$ và $\Delta CBD$có:

DA=DC(gt)

BD chung

BA=BC

Vậy $\Delta ABD = \Delta CBD$(c.c.c)

b)     Ta có $\widehat A = \widehat C = {90^o}$(hai góc tương ứng)

Theo định lí tổng ba góc trong tam giác BCD, ta có:

$\widehat C + \widehat {CDB} + \widehat {DBC} = {180^o}$

${90^o} + {30^o} + \widehat {DBC} = {180^o}$

Suy ra $\widehat {DBC} = {60^o}$

Mà $\Delta ABD = \Delta CBD$ nên $\widehat {ABD} = \widehat {CBD}$ (2 góc tương ứng)

Suy ra $\widehat {ABD} = \widehat {CBD} = {60^o}$

Do đó $\widehat {ABC} = \widehat {ABD} + \widehat {CBD} = {60^o} + {60^o} = {120^o}$