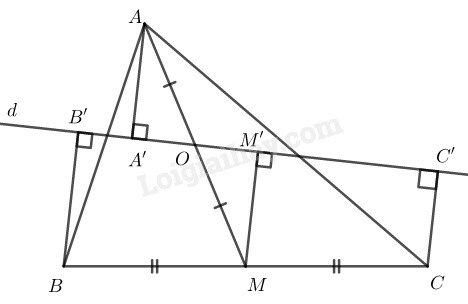
Bài 44 trang 85 SBT toán 8 tập 1Giải bài 44 trang 85 sách bài tập toán 8. Cho tam giác ABC, đường trung tuyến AM. Gọi O là trung điểm của AM. Qua O kẻ đường thẳng d cắt các cạnh AB và AC. Gọi AA’, BB’, CC’ là các đường vuông góc kẻ từ A, B, C đến đường thẳng d. Chứng minh rằng:... Đề bài Cho tam giác \(ABC,\) đường trung tuyến \(AM.\) Gọi \(O\) là trung điểm của \(AM.\) Qua \(O\) kẻ đường thẳng \(d\) cắt các cạnh \(AB\) và \(AC.\) Gọi \(AA’, BB’, CC’\) là các đường vuông góc kẻ từ \(A, B, C\) đến đường thẳng \(d.\) Chứng minh rằng: \({{AA' = }}\displaystyle {{BB' + CC'} \over 2}\) Phương pháp giải - Xem chi tiết +) Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai. +) Đường trung bình của hình thang thì song song với hai cạnh đáy và bằng nửa tổng hai đáy. Lời giải chi tiết
Ta có: \(BB’ ⊥ d\;\; (gt)\) \(CC’ ⊥ d\;\; (gt)\) Suy ra: \(BB’ // CC’\) Tứ giác \(BB’CC’\) là hình thang Kẻ \(MM’ ⊥ d\) \( ⇒ MM’ // BB’ // CC’\) Ta lại có: \(M\) là trung điểm của \(BC\) (do AM là đường trung tuyến của tam giác ABC) Nên \(MM’\) là đường trung bình của hình thang \(BB’CC’\) \( \Rightarrow MM' = \displaystyle {{BB' + CC'} \over 2}\,\,\,\,\left( 1 \right)\) Xét tam giác vuông \(AA’O\) và tam giác vuông \(MM’O:\) \(\widehat {OA'A} = \widehat {OM'M}=90^0\) \(AO = MO \;\;(gt)\) \(\widehat {AOA'} = \widehat {MOM'}\) (đối đỉnh) Do đó: \(∆ AA’O = ∆ MM’O\) (cạnh huyền, góc nhọn) \(⇒ AA’ = MM’ \;\;\;(2)\) Từ \((1)\) và \((2)\) suy ra: \({{AA' = }}\displaystyle {{BB' + CC'} \over 2}\). HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
