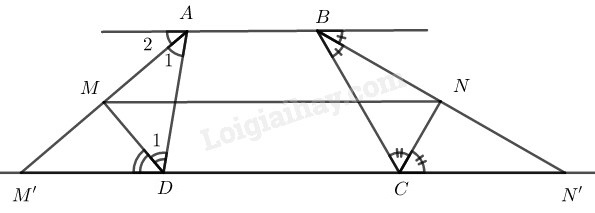
Bài 43 trang 85 SBT toán 8 tập 1

Đề bài

Hình thang $ABCD$ có $AB // CD,$ $AB = a,$ $BC = b,$ $CD = c,$ $DA = d.$ Các đường phân giác của các góc ngoài đỉnh $A$ và $D$ cắt nhau tại $M,$ các đường phân giác của các góc ngoài đỉnh $B$ và $C$ cắt nhau tại $N.$

$a)$ Chứng ninh rằng $MN // CD.$

$b)$ Tính độ dài MN theo $a, b, c, d$ ($a, b, c, d$ có cùng đơn vị đo)

Lời giải chi tiết

$a)$ Gọi $M’$ và $N’$ là giao điểm của tia $AM$ và $BN$ với $CD.$

Vì ABCD là hình thang nên $AB//CD$ hay $AB//M'N'$

Suy ra $ABN'M'$ cũng là hình thang.

Ta có:

Vì $AB//M'N'$ nên $\widehat {M'} = {\widehat A_2}$ (hai góc so le trong)

${\widehat A_1} = {\widehat A_2}$ (do AM' là phân giác góc ngoài tại đỉnh A)

Suy ra: $\widehat {M'} = {\widehat A_1}$ 

Nên $∆ ADM’$ cân tại $D$

Có $DM$ là phân giác của $\widehat {ADM'}$ 

Suy ra: $DM$ là đường trung tuyến (tính chất tam giác cân)

$⇒ AM = MM’$ (1)

Vì $AB//M'N'$ nên $\widehat {N'} = {\widehat B_2}$ (hai góc so le trong)

${\widehat B_1} = {\widehat B_2}$ (do BN' là phân giác góc ngoài tại đỉnh B)

Suy ra: $\widehat {N'} = {\widehat B_1}$ 

Nên $∆ BCN’$ cân tại $C$

Có $CN$ là phân giác của $\widehat {BCN'}$

Suy ra: $CN$ là đường trung tuyến (tính chất tam giác cân)

$⇒ BN = NN’$ (2)

Từ (1) và (2) suy ra: $MN$ là đường trung bình của hình thang $ABN’M’$

$⇒ MN // M’N’$ (tính chất đường trung bình hình thang)

Hay $MN // CD$

$b)$ $MN =\displaystyle  {{AB + M'N'} \over 2}$ (tính chất đường trung bình của hình thang)

$\Rightarrow MN = \displaystyle  {{AB + M'D + CD + CN'} \over 2}\;\,( * )$

Mà $M’D = AD$ (vì $∆ ADM’$ cân tại $D$) và $CN’ = BC$ (vì $∆ BCN’$ cân tại $C$)

Thay vào $(*)$ ta được: 

$MN = \displaystyle  {{AB + AD + CD + BC} \over 2}$$= \displaystyle {{a + d + c + b} \over 2}$

HocTot.Nam.Name.Vn