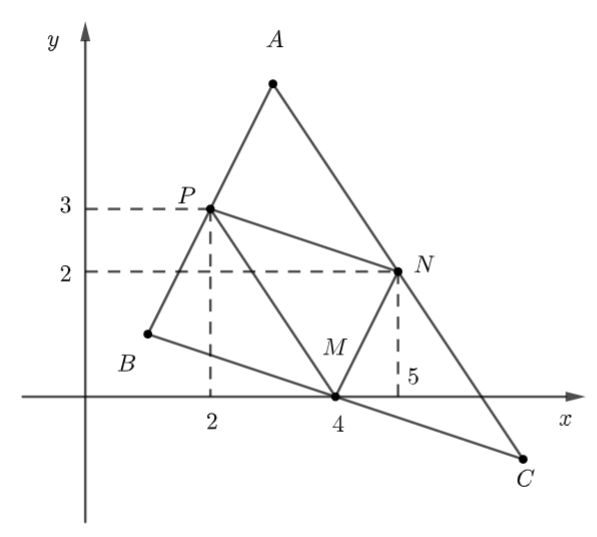
Giải bài 4.22 trang 58 sách bài tập toán 10 - Kết nối tri thức với cuộc sống

Đề bài

Trong mặt phẳng tọa độ $Oxy$ cho ba điểm $M(4;0),\,\,N(5;2)$ và $P(2;3).$ Tìm tọa độ các đỉnh của tam giác $ABC,$ biết $M,\,\,N,\,\,P$ theo thứ tự là trung điểm các cạnh $BC,\,\,CA,\,\,AB.$

Lời giải chi tiết

Ta có: $MN,\,\,NP,\,\,MP$ là đường trung bình của $\Delta ABC$

$\Rightarrow$ $MN$//$AB$, $NP$//$BC$, $MP$//$AC$.

$\Rightarrow$ $APMN$, $BPNM$, $CMPN$ là hình bình hành

Xét hình bình hành $APMN$ có:

$\begin{array}{l}\overrightarrow {OA}  = \overrightarrow {OP}  + \overrightarrow {ON}  - \overrightarrow {OM} \\ \Rightarrow \overrightarrow {OA}  = (2;3) + (5;2) - (4;0) = (3;5)\end{array}$

$\Rightarrow$ Tọa độ điểm $A$ là: $A(3;5).$

Xét hình bình hành $BPNM$ có:

$\begin{array}{l}\overrightarrow {OB}  = \overrightarrow {OP}  + \overrightarrow {OM}  - \overrightarrow {ON} \\ \Rightarrow \overrightarrow {OB}  = (2;3) + (4;0) - (5;2) = (1;1)\end{array}$

$\Rightarrow$ Tọa độ điểm $B$ là: $B(1;1).$

Xét hình bình hành $CMPN$ có:

$\begin{array}{l}\overrightarrow {OC}  = \overrightarrow {ON}  + \overrightarrow {OM}  - \overrightarrow {OP} \\ \Rightarrow \overrightarrow {OC}  = (5;2) + (4;0) - (2;3) = (7; - 1)\end{array}$

$\Rightarrow$ Tọa độ điểm $C$ là: $C(7; - 1).$