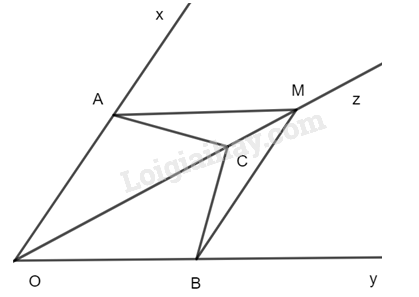
Giải bài 4.19 trang 74 SGK Toán 7 tập 1 - Kết nối tri thức

Đề bài

Cho tia Oz là tia phân giác của góc xOy. Lấy các điểm A,B,C lần lượt thuộc các tia Ox, Oy, Oz sao cho $\widehat {CAO} = \widehat {CBO}.$

a) Chứng minh rằng $\Delta OAC = \Delta OBC$.

b) Lấy điểm $M$ trên tia đối của tia CO. Chứng minh rằng $\Delta MAC = \Delta MBC$.

Lời giải chi tiết

a) Trong $\Delta OAC$ có: $\widehat {AOC}+\widehat {OAC}+\widehat {OCA}=180^0$

Trong $\Delta OBC$ có: $\widehat {BOC}+\widehat {OBC}+\widehat {OCB}=180^0$

Mà $\widehat {AOC} = \widehat {BOC}$(do Oz là phân giác góc xOy) và $\widehat {CAO}=\widehat {CBO}$ 

Do đó, $\widehat {OCA}=\widehat {OCB}$.

Xét $\Delta OAC$ và $\Delta OBC$ có:

$\widehat {AOC} = \widehat {BOC}$ (cmt)

OC chung

$\widehat {OCA} = \widehat {OCB}(cmt)$

$\Rightarrow \Delta OAC = \Delta OBC$(g.c.g)

b) Do $\Delta OAC = \Delta OBC$ nên AC=BC ( 2 cạnh tương ứng)

Vì $\widehat {ACO}$ và $\widehat {ACM}$ kề bù

    $\widehat {BCO}$ và $\widehat {BCM}$ kề bù

Mà $\widehat {ACO} = \widehat {BCO}$ nên $\widehat {ACM} = \widehat {BCM}$

Xét $\Delta MAC$ và $\Delta MBC$ có:

AC=BC (cmt)

$\widehat {ACM} = \widehat {BCM}$ (cmt)

CM chung

$\Rightarrow \Delta MAC = \Delta MBC$(c.g.c)