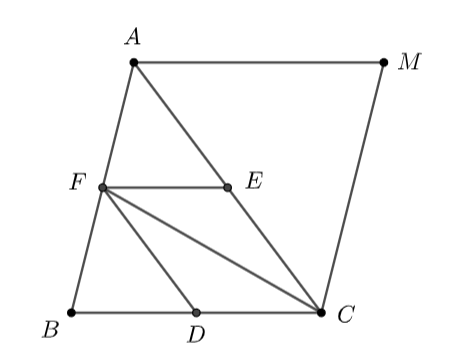
Giải bài 4.10 trang 51 sách bài tập toán 10 - Kết nối tri thức với cuộc sống

Đề bài

Cho tam giác $ABC.$ Gọi $D,\,\,E,\,\,F$ theo thứ tự là trung điểm của các cạnh $BC,\,\,CA,\,\,AB.$

a) Xác định vectơ $\overrightarrow {AF}  - \overrightarrow {BD}  + \overrightarrow {CE}$

b) Xác định điểm $M$ thỏa mãn $\overrightarrow {AF}  - \overrightarrow {BD}  + \overrightarrow {CE}  = \overrightarrow {MA} .$

c) Chứng minh rằng $\overrightarrow {MC}  = \overrightarrow {AB} .$

Lời giải chi tiết

a)      Ta có: $DF$ là đường trung bình của $\Delta ABC$

$\Rightarrow$ $\overrightarrow {CE}  = \overrightarrow {DF}$

$\Rightarrow$ tứ giác $CDFE$ là hình bình hành.

Ta có: $D$ và $F$ lần lượt là trung điểm của $BC$ và $AB$

$\Rightarrow$ $\overrightarrow {AF}  = \overrightarrow {FB} ,$ $\overrightarrow {BD}  = \overrightarrow {DC}$ 

Ta có: $\overrightarrow {AF}  - \overrightarrow {BD}  + \overrightarrow {CE}  = \overrightarrow {AF}  + \overrightarrow {CD}  + \overrightarrow {CE}  = \overrightarrow {AF}  + \overrightarrow {CF}  = \overrightarrow {CF}  + \overrightarrow {FB}  = \overrightarrow {CB}$

b)     Theo câu a, ta có: $\overrightarrow {AF}  - \overrightarrow {BD}  + \overrightarrow {CE}  = \overrightarrow {CB}$

mặt khác $\overrightarrow {AF}  - \overrightarrow {BD}  + \overrightarrow {CE}  = \overrightarrow {MA} .$

nên $\overrightarrow {CB}  = \overrightarrow {MA}$

$\Rightarrow$ tứ giác $ABCM$ là hình bình hành

$\Rightarrow$ $M$ là điểm đối xứng với $B$ qua $E$

c)      Theo câu b, ta có: tứ giác $ABCM$ là hình bình hành

$\Rightarrow$ $\overrightarrow {MC}  = \overrightarrow {AB} .$