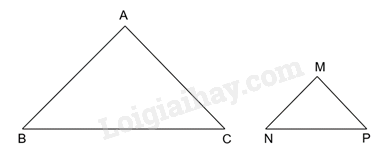
Giải bài 4 trang 84 vở thực hành Toán 8 tập 2Cho tam giác ABC cân tại đỉnh A và tam giác MNP cân tại đỉnh M. Biết rằng widehatBAC=widehatPMN, AB=2MN. Tổng hợp đề thi học kì 2 lớp 8 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên Đề bài Cho tam giác ABC cân tại đỉnh A và tam giác MNP cân tại đỉnh M. Biết rằng ^BAC=^PMN, AB=2MN. Chứng minh ΔMNP ∽ ΔABC và tìm tỉ số đồng dạng .
Phương pháp giải - Xem chi tiết Sử dụng tam giác ABC cân tại A, tam giác MNP cân tại M để chứng minh ΔMNP ∽ ΔABC và tìm tỉ số đồng dạng của chúng. Lời giải chi tiết Vì ΔABC cân nên ^ABC=^ACB=^ABC+^ACB2=180o−^BAC2 (1). Tương tự, ΔMNP cân tại M nên ^MNP=180o−^PMN2 (2). Vì ^BAC=^PMN nên từ (1) và (2) ta suy ra ^ABC=^MNP. Lấy B’, C’ lần lượt là trung điểm của AB, AC thì ta có B’C’ // BC. Do đó ^ABC=^AB′C′,^ACB=^AC′B′ (các cặp góc đồng vị). Hai tam giác AB’C’ và MNP có: ^BAC=^NMP (theo giả thiết), AB′=AB2=MN (theo giả thiết), ^AB′C′=^ABC=^MNP (theo chứng minh trên). Vậy ΔMNP = ΔAB’C’ (g.c.g). Mặt khác, ΔAB’C’ ∽ ΔABC ( vì B’C’ // BC). Do đó ΔMNP ∽ ΔABC với tỉ số đồng dạng k=AB′AB=12.
|