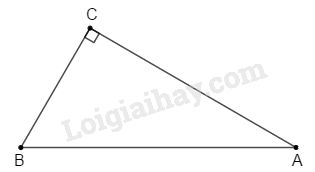
Bài 4 trang 196 SBT toán 9 tập 2

Đề bài

Tính sin, cos, tang của các góc $A$ và $B$ của tam giác $ABC$ vuông ở $C$ biết:

a) $BC= 8, AB = 17;$

b) $BC=21,AC=20;$

c) $BC=1,AC=2;$

d) $AC=24,AB=25.$

Lời giải chi tiết

a) Áp dụng định lí Pytago vào tam giác $ABC$ vuông tại $C$, ta có:

$A{B^2} = B{C^2} + A{C^2}$

$\Rightarrow AC = \sqrt {A{B^2} - B{C^2}} = \sqrt {{{17}^2} - {8^2}}$$\,= 15$

Tam giác $ABC$ vuông tại $C$ nên $\widehat A$ và $\widehat B$ là hai góc phụ nhau, ta có:

$\begin{array}{l} \sin A = \cos B = \dfrac{{BC}}{{AB}} = \dfrac{8}{{17}}\\ \cos A = \sin B = \dfrac{{CA}}{{AB}} = \dfrac{{15}}{{17}}\\ \tan A = \cot B = \dfrac{{BC}}{{AC}} = \dfrac{8}{{15}}\\ \cot A = \tan B = \dfrac{{AC}}{{BC}} = \dfrac{{15}}{8} \end{array}$

b) Áp dụng định lí Pytago vào tam giác $ABC$ vuông tại $C$, ta có:

$A{B^2} = B{C^2} + A{C^2} = {21^2} + {20^2}$$\, = 841$

$\Rightarrow AB = \sqrt {841} = 29$.

Tam giác $ABC$ vuông tại $C$ nên $\widehat A$ và $\widehat B$ là hai góc phụ nhau, ta có:

$\begin{array}{l} \sin A = \cos B = \dfrac{{BC}}{{AB}} = \dfrac{{21}}{{29}}\\ \cos A = \sin B = \dfrac{{AC}}{{AB}} = \dfrac{{20}}{{29}}\\ \tan A = \cot B = \dfrac{{BC}}{{AC}} = \dfrac{{21}}{{20}}\\ \cot A = \tan B = \dfrac{{AC}}{{BC}} = \dfrac{{20}}{{21}} \end{array}$

c) Áp dụng định lí Pytago vào tam giác $ABC$ vuông tại $C$, ta có:

$\begin{array}{l} A{B^2} = B{C^2} + A{C^2} = {1^2} + {2^2} = 5\\ \Rightarrow AB = \sqrt 5 \end{array}$

Tam giác $ABC$ vuông tại $C$ nên $\widehat A$ và $\widehat B$ là hai góc phụ nhau, ta có:

$\begin{array}{l} \sin A = \cos B = \dfrac{{BC}}{{AB}} = \dfrac{1}{{\sqrt 5 }}\\ \cos A = \sin B = \dfrac{{AC}}{{AB}} = \dfrac{2}{{\sqrt 5 }}\\ \tan A = \cot B = \dfrac{{BC}}{{AC}} = \dfrac{1}{2}\\ \cot A = \tan B = \dfrac{{AC}}{{BC}} = \dfrac{2}{1} = 2 \end{array}$

d) Áp dụng định lí Pytago vào tam giác $ABC$ vuông tại $C$, ta có:

$A{B^2} = B{C^2} + A{C^2}$

$\Rightarrow BC = \sqrt {A{B^2} - A{C^2}}$$\,= \sqrt {{{25}^2} - {{24}^2}}$$\, = \sqrt {49}  = 7$

Tam giác $ABC$ vuông tại $C$ nên $\widehat A$ và $\widehat B$ là hai góc phụ nhau, ta có:

$\begin{array}{l} \sin A = \cos B = \dfrac{{BC}}{{AB}} = \dfrac{7}{{25}}\\ \cos A = \sin B = \dfrac{{AC}}{{AB}} = \dfrac{{24}}{{25}}\\ \tan A = \cot B = \dfrac{{BC}}{{AC}} = \dfrac{7}{{24}}\\ \cot A = \tan B = \dfrac{{AC}}{{BC}} = \dfrac{{24}}{7} \end{array}$

HocTot.Nam.Name.Vn