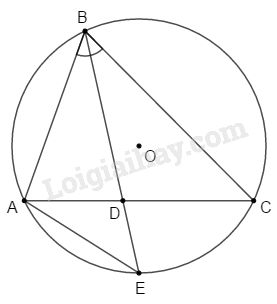
Bài 5 trang 196 SBT toán 9 tập 2

Đề bài

\(BD\) là đường phân giác của tam giác \(ABC.\) Chứng minh rằng \(BD^2=AB.BC - AD.DC.\)

Lời giải chi tiết

Gọi \(E\) là giao điểm của tia \(BD\) và đường tròn ngoại tiếp \(\Delta ABC\).

* Xét \(\Delta BEA\) và \(\Delta BCD\) có:

\(\widehat {ABE} = \widehat {DBC}\) (vì \(BD\) là tia phân giác \(\widehat B\))

\(\widehat {BEA} = \widehat {BCD}\) (hai góc nội tiếp cùng chắn cung \(AB\))

\(\Rightarrow \Delta BEA\backsim \Delta BCD\) (g.g)

\( \Rightarrow \dfrac{{AB}}{{BD}} = \dfrac{{BE}}{{BC}}\)

Mà \(BE=BD+DE\) nên \(\dfrac{{AB}}{{BD}} = \dfrac{{BD + DE}}{{BC}}\)

\(\Rightarrow B{D^2} + BD.DE = AB.BC\)

\( \Rightarrow B{D^2} = AB.BC - BD.DE\)    (1)

* Xét \(\Delta BDC\) và \(\Delta ADE\) có:

\(\widehat {BDC} = \widehat {ADE}\) (hai góc đối đỉnh)

\(\widehat {DBC} = \widehat {DAE}\) (hai góc nội tiếp cùng chắn cung \(CE\))

\(\Rightarrow \Delta BDC\backsim \Delta ADE\) (g.g)

\(\Rightarrow \dfrac{{BD}}{{DC}} = \dfrac{{AD}}{{DE}}\)

\(\Rightarrow BD.DE = AD.DC\)          (2)

Từ (1) và (2) suy ra: \(B{D^2} = AB.BC - AD.DC\) (điều phải chứng minh).

HocTot.Nam.Name.Vn