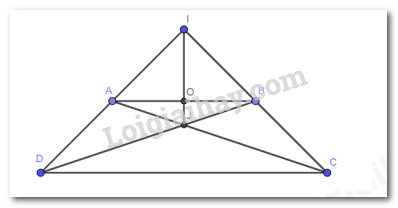
Giải bài 3.8 trang 55 SGK Toán 8 tập 1 - Kết nối tri thứcHình thang cân ABCD (AB // CD, AB < CD) có Tổng hợp đề thi học kì 1 lớp 8 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên Đề bài Hình thang cân ABCD (AB // CD, AB < CD) có các đường thẳng AD, BC cắt nhau tại I, các đường thẳng AC, BD cắt nhau tại J. Chứng minh rằng đường thẳng IJ là đường trung trực của đoạn thẳng AB. Video hướng dẫn giải Phương pháp giải - Xem chi tiết Gọi O là giao điểm của AB và IJ Chứng minh: Tam giác IAB cân tại I (vì IA = IB) có IO là tia phân giác \(\widehat {AIB}\) Suy ra IO là đường trung trực của đoạn thẳng AB. Suy ra đường thẳng IJ là đường trung trực của đoạn thẳng AB Lời giải chi tiết
Gọi O là giao điểm của AB và IJ. Vì ABCD là hình thang cân nên \(\widehat {BA{\rm{D}}} = \widehat {ABC};\widehat {A{\rm{D}}C} = \widehat {BC{\rm{D}}};A{\rm{D}} = BC, AC = BD\) Tam giác ICD cân tại I (vì \(\widehat {A{\rm{D}}C} = \widehat {BC{\rm{D}}}\)) nên IC = ID. Xét tam giác ABD và BAC có: AB chung AD = BC (cmt) AC = BD (cmt) => ∆ABD = ∆BAC (c.c.c) => \(\widehat {A{\rm{D}}B} = \widehat {BC{\rm{A}}}\) Vì \(\widehat {A{\rm{D}}C} = \widehat {BC{\rm{D}}};\widehat {A{\rm{D}}B} = \widehat {BC{\rm{A}}}\) nên \(\widehat {J{\rm{D}}C} = \widehat {JC{\rm{D}}}\) Tam giác JCD cân tại J (vì \(\widehat {J{\rm{D}}C} = \widehat {JC{\rm{D}}}\) ) nên JC = JD. Xét ∆IJD và ∆IJC có: IC = ID (chứng minh trên); \(\widehat {A{\rm{D}}B} = \widehat {BC{\rm{A}}}\); JC = JD (chứng minh trên). Do đó ∆IJD = ∆IJC (c.g.c). Suy ra \(\widehat {D{\rm{IJ}}} = \widehat {C{\rm{IJ}}}\) (hai góc tương ứng). Ta có ID = IC, AD = BC. Mà ID = AI + AD; IC = IB + BC nên IA = IB. Tam giác IAB cân tại I (vì IA = IB) có IO là tia phân giác \(\widehat {AIB}\) Suy ra IO là đường trung trực của đoạn thẳng AB. Vậy đường thẳng IJ là đường trung trực của đoạn thẳng AB.
|