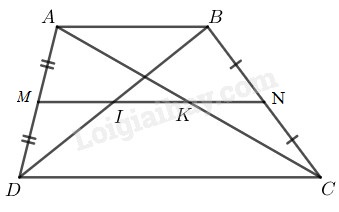
Bài 37 trang 84 SBT toán 8 tập 1Giải bài 37 trang 84 sách bài tập toán 8. Cho hình thang ABCD (AB // CD), M là trung điểm của AD, N là trung điểm của BC. Gọi I, K theo thứ tự là giao điểm của MN với BD, AC. Cho biết AB = 6cm, CD = 14 cm. Tính các độ dài MI, IK, KN. Đề bài Cho hình thang \(ABCD\) \((AB // CD),\) \(M\) là trung điểm của \(AD,\) \(N\) là trung điểm của \(BC.\) Gọi \(I, K\) theo thứ tự là giao điểm của \(MN\) với \(BD, AC.\) Cho biết \(AB = 6\,cm,\) \(CD = 14 cm.\) Tính các độ dài \(MI, IK, KN.\) Phương pháp giải - Xem chi tiết Sử dụng định nghĩa, tính chất đường trung bình của tam giác và hình thang: +) Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác. +) Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang. +) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy. +) Đường trung bình của hình thang thì song song với hai cạnh đáy và bằng nửa tổng hai đáy. +) Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba. Lời giải chi tiết
Hình thang \(ABCD\) có \(AB // CD\) \(M\) là trung điểm của \(AD\;\; (gt)\) \(N\) là trung điểm của \(BC\;\; (gt)\) Nên \(MN\) là đường trung bình của hình thang \(ABCD\) \(⇒ MN // AB // CD\) và \(MN =\displaystyle {{AB + CD} \over 2} = {{6 + 14} \over 2} = 10\left( {cm} \right)\) Trong tam giác \(ADC\) ta có: \(M\) là trung điểm của \(AD\) \(MK // CD\) \(⇒ AK = KC\) (đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba) Suy ra \(MK\) là đường trung bình của \(∆ ADC.\) \( \Rightarrow MK = \displaystyle {1 \over 2}CD = {1 \over 2}.14 = 7\left( {cm} \right)\) Vậy: \(KN = MN – MK = 10 – 7 = 3 \;\;(cm)\) Trong \(∆ ADB\) ta có: \(M\) là trung điểm của \(AD\) \(MI // AB\) Nên \(DI = IB\) (đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba) \(⇒ MI\) là đường trung bình của \(∆ DAB\) \( \Rightarrow MI =\displaystyle {1 \over 2}AB = {1 \over 2}.6 = 3\left( {cm} \right)\) \(IK = MK – MI = 7 – 3 = 4\;\; (cm)\) HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
