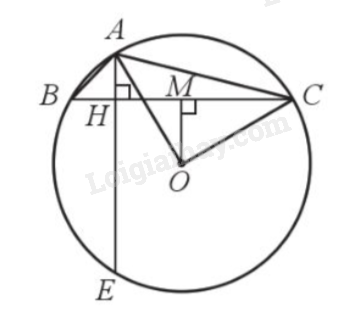
Giải bài 36 trang 117 sách bài tập toán 9 - Cánh diều tập 1

Đề bài

Cho đường tròn (O; 1dm) và ba điểm A, B, C nằm trên đường tròn sao cho $\widehat {ABC} = 45^\circ$, $\widehat {ACB} = 15^\circ$. Kẻ AH vuông góc với BC tại H, tia AH cắt đường tròn (O) tại E (Hình 36). Tính:

a) Số đo cung nhỏ CE và số đo cung lớn BC;

b) Độ dài các đoạn thẳng AC, BC.

Lời giải chi tiết

Kẻ OM vuông góc với BC tại M, suy ra $\widehat {BMO} = \widehat {MCO} = 90^\circ$.

a) Xét tam giác HAC vuông tại H có $\widehat {HAC} + \widehat {ACH} = 90^\circ$ hay $\widehat {HAC} = 90^\circ  - \widehat {ACH} = 90^\circ  - 15^\circ  = 75^\circ$

Mặt khác, $\widehat {HAC}$ là góc nội tiếp chắn cung nhỏ EC nên số đo cung nhỏ EC là $2.\widehat {HAC} = 2.75^\circ  = 150^\circ$.

Xét tam giác ABC có $\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = 180^\circ$ hay

$\widehat {BAC} = 180^\circ  - \left( {\widehat {ABC} + \widehat {ACB}} \right) \\= 180^\circ  - \left( {45^\circ  - 15^\circ } \right) \\= 120^\circ$

mà $\widehat {BAC}$ là góc nội tiếp chắn cung lớn BC nên số đo cung lớn BC là $2.\widehat {BAC} = 2.120^\circ  = 240^\circ$.

b) Ta có góc ABC nội tiếp chắn cung AC của (O), mà $\widehat {ABC} = 45^\circ$ nên số đo cung AC là $2.\widehat {ABC} = 2.45^\circ  = 90^\circ$.

Do đó góc ở tâm chắn cung AC là góc AOC có số đo bằng $90^\circ$.

Xét tam giác OAC có $OA = OC = 1$dm (cùng bằng bán kính (O)), $\widehat {AOC} = 90^\circ$ suy ra tam giác OAC vuông cân tại O, do đó $CA = \sqrt {O{A^2} + O{C^2}}$ (Định lí Pythagore) hay $CA = \sqrt {{1^2} + {1^2}}  = \sqrt 2$dm.

Xét 2 tam giác OBM và OCM có

$OB = OC$ (cùng bằng bán kính (O))

OM chung

$\widehat {BMO} = \widehat {MCO} = 90^\circ$

Suy ra $\Delta OBM = \Delta OCM$ (cạnh huyền – cạnh góc vuông), do đó $BM = CM = \frac{{BC}}{2}$.

Ta có $\Delta OAC$ vuông cân nên $\widehat {OCA} = 45^\circ$. Ta lại có $\widehat {OCM} = \widehat {OCA} - \widehat {ACB} = 45^\circ  - 15^\circ  = 30^\circ$

Mặt khác, tam giác OCM vuông tại M nên $CM = OC.\cos \widehat {OCM} = 1.\cos 30^\circ  = \frac{{\sqrt 3 }}{2}$dm.

Vậy $BC = 2CM = 2.\frac{{\sqrt 3 }}{2} = \sqrt 3$dm.