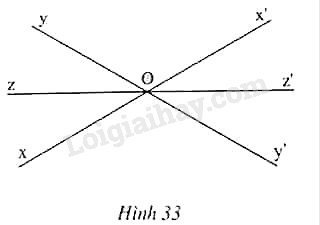
Bài 34 trang 83 Vở bài tập toán 7 tập 2Giải bài 34 trang 83, 84 VBT toán 7 tập 2. Cho hai đường thẳng xx’ và yy’ cắt nhau tại O (h.33). Chứng minh rằng : a) Nếu Oz là tia phân giác của góc xOy ... Đề bài Cho hai đường thẳng xx′ và yy′ cắt nhau tại O (h.33). Chứng minh rằng: a) Nếu Oz là tia phân giác của góc xOy thì tia đối của tia Oz sẽ là tia phân giác của góc x′Oy′. b) Tập hợp các điểm nằm bên trong hai góc xOy và x′Oy′, cách đều hai đường thẳng xx′ và yy′ là đường thẳng zz′.
Phương pháp giải - Xem chi tiết Vận dụng kiến thức : Tập hợp các điểm nằm bên trong một góc và cách đều hai cạnh của góc là tia phân giác của góc đó. Lời giải chi tiết GT: xx′∩yy′={O}, Oz,Oz′ là hai tia đối nhau KL: a) Nếu Oz là phân giác của ^xOy thì Oz′ là phân giác của ^x′Oy′ b) Tập hợp các điểm nằm bên trong hai góc xOy và x′Oy′, cách đều hai đường thẳng xx′ và yy′ là đường thẳng zz′. Giải: a) Vì Oz là tia phân giác của góc xOy nên Oz nằm giữa tia Ox; Oy và ^zOy=^zOx. Từ đó suy ra Oz′ (tia đối của tia Oz) nằm giữa Ox′ và Oy′. Mặt khác, ^zOy=^z′Oy′ (đối đỉnh), ^zOx=^z′Ox′ (đối đỉnh) mà ^xOy=^x′Oy′ nên suy ra ^x′Oz′=^y′Oz′. Vậy Oz′ là tia phân giác của góc x′Oy′. b) Theo tính chất tia phân giác, ta có: - Tập hợp các điểm nằm bên trong góc xOy (cũng cách đều hai đường thẳng xx′, yy′) là tia phân giác Oz; - Tập hợp các điểm nằm bên trong góc x′Oy′ (cũng cách đều hai đường thẳng xx′, yy′) là tia phân giác Oz′; Vậy tập hợp các điểm nằm bên trong hai góc xOy và x′Oy′, cách đều hai đường thẳng xx′ và yy′ là đường thẳng zz′. HocTot.Nam.Name.Vn
|