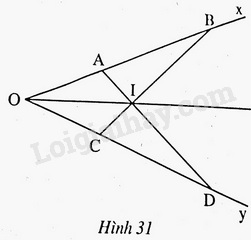
Bài 32 trang 82 Vở bài tập toán 7 tập 2Giải bài 32 trang 82, 83 VBT toán 7 tập 2. Cho góc xOy khác góc bẹt. Trên tia Ox lấy hai điểm A và B, trên tia Oy lấy hai điểm C và D sao cho OA = OC; OB = OD... Đề bài Cho góc xOy khác góc bẹt. Trên tia Ox lấy hai điểm A và B, trên tia Oy lấy hai điểm C và D sao cho OA=OC,OB=OD. Gọi I là giao điểm của hai đoạn thẳng AD và BC. Chứng minh rằng: a) BC=AD b) IA=IC,IB=ID c) Tia OI là tia phân giác của góc xOy. Phương pháp giải - Xem chi tiết Chứng minh dựa vào các tam giác bằng nhau. Lời giải chi tiết
a) Xét hai tam giác OAD và OCB. Ta có OA=OC (gt); OD=OB (gt), góc O chung Vậy ∆AOD=∆COB (c.g.c) suy ra AD=BC (hai cạnh tương ứng). b) Xét hai tam giác AIB và CID. Ta có (theo gt) AB=OB−OA=OD−OC=CD. Mặt khác, do ∆AOD=∆COB (câu a) suy ra ^ABI=^CDI và ^OAI=^OCI. Từ ^OAI=^OCI suy ra ^BAI=^DCI (cặp góc kề bù với các góc bằng nhau) Vậy ∆AIB=∆CID (g.c.g) suy ra IC=IA và ID=IB (hai cạnh tương ứng) c) Ta có ∆OBI=∆ODI (c.c.c), suy ra ^AOI=^COI. Hơn nữa, hiển nhiên I nằm bên trong góc xOy. Vậy OI là tia là phân giác của ^xOy. HocTot.Nam.Name.Vn
|