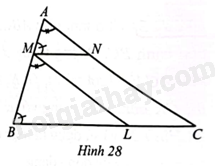
Giải bài 28 trang 70 sách bài tập toán 8 – Cánh diềuQuan sát Hình 28 biết \(\widehat{AMN}=\widehat{ABC},\widehat{BAC}=\widehat{BML}\). Đề bài Quan sát Hình 28 biết \(\widehat{AMN}=\widehat{ABC},\widehat{BAC}=\widehat{BML}\). a) Chứng minh: \(\Delta AMN\backsim \Delta MBL\). b) Xác định vị trí của điểm \(M\) trên cạnh \(AB\) để chu vi tam giác \(AMN\) bằng \(\frac{2}{3}\) chu vi tam giác \(ABC\). Phương pháp giải - Xem chi tiết Dựa vào định nghĩa của tam giác đồng dạng: Tam giác \(A'B'C'\) gọi là đồng dạng với tam giác \(ABC\) nếu: \(\widehat{A'}=\widehat{A},\widehat{B'}=\widehat{B},\widehat{C'}=\widehat{C}\) ; \(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{A'C'}{AC}\). Kí hiệu là \(\Delta A'B'C'\backsim \Delta ABC\). Tỉ số các cạnh tương ứng \(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}=k\) gọi là tỉ số đồng dạng. Và công thức tính chu vi tam giác. Lời giải chi tiết a) Vì \(\widehat{AMN}=\widehat{ABC}\) nên \(MN//BC\). Do đó \(\Delta AMN\backsim \Delta ABC\) (1) Vì \(\widehat{BAC}=\widehat{BML}\) nên \(ML//AC\). Do đó \(\Delta MBL\backsim \Delta ABC\) (2) Từ (1) và (2) ta có \(\Delta AMN\backsim \Delta MBL\), b) Giả sử \(\Delta AMN\backsim \Delta ABC\) với tỉ số đồng dạng \(k\), ta có: \(\frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC}=k\). → \(\frac{AM}{AB}=\frac{AN}{AC}=\frac{MN}{BC}=\frac{AM+AN+MN}{AB+AC+BC}=k\) hay (Chu vi tam giác \(AMN\)) : (Chu vi tam giác \(ABC\)) \(=k\). Do đó để chu vi tam giác \(AMN\) bằng \(\frac{2}{3}\) chu vi tam giác \(ABC\) thì \(AM=\frac{2}{3}AB\). Ngược lại, dễ thấy nếu \(AM=\frac{2}{3}AB\) thì chu vi tam giác \(AMN\) bằng \(\frac{2}{3}\) tam giác \(ABC\). Vậy vị trí của điểm \(M\) trên cạnh \(AB\) để chu vi tam giác \(AMN\) bằng chu vi tam giác \(ABC\) là \(AM=\frac{2}{3}AB\).  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
