Bài 26 trang 83 SBT toán 8 tập 1

Đề bài

Chứng minh rằng hình thang có hai đường chéo bằng nhau là hình thang cân.

Lời giải chi tiết

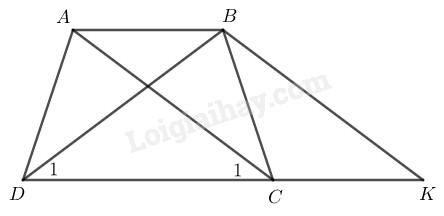
Giả sử ABCD là hình thang có hai đường chéo \(AC=BD\). Ta chứng minh \(ABCD\) là hình thang cân.

Từ \(B\) kẻ đường thẳng song song với \(AC\) cắt đường thẳng \(DC\) tại \(K.\)

Ta có hình thang \(ABKC\) (do AB//CK) có hai cạnh bên \(BK // AC\) nên \(AC = BK\)

Mà \(AC = BD \;\;\; (gt)\)

Suy ra: \(BD = BK\) do đó \(∆ BDK\) cân tại \(B\)

\( \Rightarrow {\widehat D_1} = \widehat K\) (tính chất tam giác cân)

Ta lại có: \({\widehat C_1} = \widehat K\) (hai góc đồng vị)

Suy ra:  \({\widehat D_1} = {\widehat C_1}\)

Xét \(∆ ACD\) và \(∆ BDC:\)

\(AC = BD \;\;\; (gt)\)

\({\widehat D_1} = {\widehat C_1}\) (chứng minh trên)

\(CD\) cạnh chung

Do đó: \(∆ ACD = ∆ BDC\;\;\; (c.g.c)\) \( \Rightarrow \widehat {ADC} = \widehat {BCD}\)   

Hình thang \(ABCD\) có \(\widehat {ADC} = \widehat {BCD}\) nên là hình thang cân.

HocTot.Nam.Name.Vn