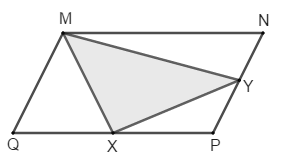
Bài 2.6 phần bài tập bổ sung trang 167 SBT toán 8 tập 1Giải bài 2.6 phần bài tập bổ sung trang 167 sách bài tập toán 8. Cho hình bs.30 (hình bình hành MNPQ có diện tích S và X, Y tương ứng là trung điểm của các cạnh QP, PN). Khi đó, diện tích của tứ giác MXPY bằng: Đề bài Cho hình bs.30 (hình bình hành \(MNPQ\) có diện tích \(S\) và \(X,\, Y\) tương ứng là trung điểm của các cạnh \(QP, PN).\) Khi đó, diện tích của tứ giác \(MXPY\) bằng: (A) \(\dfrac {1}{4}S\) (B) \(\dfrac {1}{2}S\) (C) \(\dfrac {1}{8}S\) (D) \(\dfrac {3}{4}S\)
Phương pháp giải - Xem chi tiết Dựa vào công thức tính diện tích tam giác bằng nửa tích chiều cao và cạnh đáy tương ứng: \(S=\dfrac {1}{2}ah\) Lời giải chi tiết Theo bài ra ta có: \(X,\, Y\) tương ứng là trung điểm của các cạnh \(QP, PN\) nên \(QX=XP\) và \(NY=PY\) Có \(S_{MQX}=S_{MXP}\) vì hai tam giác chung đường cao kẻ từ \(M\) và có cạnh đáy bằng nhau. Suy ra: \(S_{MXP}=\dfrac{1}{2} S_{MQP}\) \(S_{MYP}=S_{MYN}\) vì hai tam giác chung đường cao kẻ từ \(M\) và có cạnh đáy bằng nhau. Suy ra: \(S_{MYP}=\dfrac{1}{2} S_{MPN}\) Mà \(S_{MQP}+S_{MPN}=S_{MNPQ}\) nên \(S_{MXP}+S_{MYP}=\dfrac{1}{2}S_{MNPQ}\) hay \(S_{MXPY}=\dfrac{1}{2}S\) Chọn (B) HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
