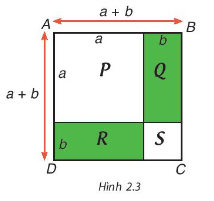
Giải bài 2.35 trang 47 SGK Toán 8 tập 1 - Kết nối tri thứchãy giải thích hằng đẳng thức Tổng hợp đề thi học kì 1 lớp 8 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Khoa học tự nhiên Đề bài Sử dụng Hình 2.3, bằng cách tính diện tích hình vuông ABCD theo hai cách, hãy giải thích hằng đẳng thức \({\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}\). Video hướng dẫn giải Phương pháp giải - Xem chi tiết Cách 1: Diện tích hình vuông bằng bình phương một cạnh. Cách 2: Diện tích ABCD = Diện tích P + Q + R + S Lời giải chi tiết Diện tích hình vuông ABCD là: \({\left( {a + b} \right)^2}\) Diện tích hình vuông ABCD là: \({S_{ABCD}} = {S_P} + {S_Q} + {S_R} + {S_S} \) \(= {a^2} + ab + ab + {b^2} \) \(= {a^2} + 2ab + {b^2}\) Do đó \({\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}\)
|