Bài 2.2 phần bài tập bổ sung trang 159 SBT toán 8 tập 1

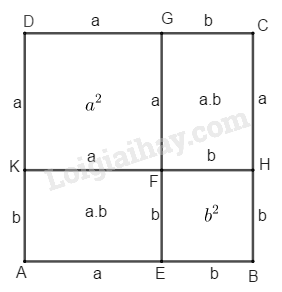
LG a

Dùng diện tích để chứng tỏ : \({\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}\)

Phương pháp giải:

Dựng hình vuông rồi lấy các điểm và đặt độ dài sao cho phù hợp.

Sau đó áp dụng công thức tính diện tích hình chữ nhật : \(S=ab\)

Lời giải chi tiết:

Dựng hình vuông \(ABCD\) có cạnh bằng \((a + b )\)

Trên cạnh \(AB\) dựng điểm \(E\) sao cho \(AE = a,\, EB = b,\) trên cạnh \(BC\) dựng điểm \(H\) sao cho \(BH = b,\, HC = a,\) trên cạnh \(CD\) dựng điểm \(G\) sao cho \(CG = b,\, GD = a,\) trên cạnh \(DA\) dựng điểm \(K\) sao cho \(DK = a,\, KA = b,\) \(GE\) cắt \(KH\) tại \(F.\)

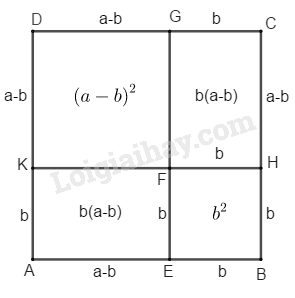
Ta có : diện tích hình vuông \(ABCD\) bằng \({\left( {a + b} \right)^2}\)

Diện tích hình vuông \(DKFG\) bằng \({a^2}\)

Diện tích hình chữ nhật \(AKFE\) bằng \(a.b\)

Diện tích hình vuông \(EBHF\) bằng \({b^2}\)

Diện tích hình chữ nhật \(HCGF\) bằng \(a.b\)

\({S_{ABCD}} = {S_{DKFG}} + {S_{AKFE}}\) \(+ {S_{EBHF}}\) \(+ {S_{HCGF}}\)

Vậy ta có : \({\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}\)

LG b

Dùng diện tích để chứng tỏ : \({\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}\)với điều kiện \(b < a\)

Phương pháp giải:

Dựng hình vuông rồi lấy các điểm và đặt độ dài sao cho phù hợp.

Sau đó áp dụng công thức tính diện tích hình chữ nhật : \(S=ab\)

Lời giải chi tiết:

Dựng hình vuông \(ABCD\) có cạnh bằng \(a\)

Trên cạnh \(AB\) lấy điểm \(E\) sao cho \(BE = b\)

Từ \(E\) dựng đường thẳng song song \(BC\) cắt \(CD\) tại \(G\)

Ta có: \(CG = b,\) \(CE = ( a – b ),\) \(GD = ( a – b )\)

Trên cạnh \(AD\) lấy điểm \(K\) sao cho \(AK = b\)

Từ \(K\) kẻ đường thẳng song song với \(AB\) cắt \(BC\) tại \(H\) và cắt \(EG\) tại \(F\)

Ta có: \(KD = ( a – b ),\) \(BH = b\)

Hình vuông \(ABCD\) có diện tích bằng \({a^2}\)

Hình vuông \(DKFG\) có diện tích bằng \({\left( {a - b} \right)^2}\)

Hình chữ nhật \(AEFK\) có diện tích bằng \(( a – b ). b\)

Hình vuông \(EBHF\) có diện tích bằng \({b^2}\)

Hình chữ nhật \(HCGF\) có diện tích bằng \(( a – b ).b\)

\({S_{ABCD}} = {S_{DKFG}} + {S_{AEFK}}\) \(+ {S_{EBHF}} + {S_{HCGF}}\)

nên \({\left( {a - b} \right)^2} + \left( {a - b} \right)b\) \(+ \left( {a - b} \right)b + {b^2} = {a^2}\)

\(\begin{array}{l}
\Leftrightarrow {\left( {a - b} \right)^2} + ab - {b^2} + ab - {b^2} + {b^2} = {a^2}\\
\Leftrightarrow {\left( {a - b} \right)^2} + 2ab - {b^2} = {a^2}\\
\Leftrightarrow {\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}
\end{array}\)

Vậy \( {\left( {a - b} \right)^2} = {a^2} - 2ab + {b^2}\)

HocTot.Nam.Name.Vn