Bài 2.17 trang 71 SBT hình học 11Giải bài 2.17 trang 71 sách bài tập hình học 11. Cho hai hình bình hành ABCD và ABEF nằm trong hai mặt phẳng phân biệt. Gọi O là giao điểm của AC và BD, O’ là giao điểm của AE và BF... GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT Gửi góp ý cho HocTot.Nam.Name.Vn và nhận về những phần quà hấp dẫn
Lựa chọn câu để xem lời giải nhanh hơn
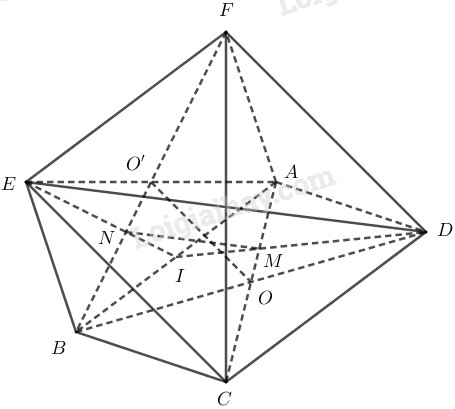
Cho hai hình bình hành \(ABCD\) và \(ABEF\) nằm trong hai mặt phẳng phân biệt. Gọi \(O\) là giao điểm của \(AC\) và \(BD\), \(O’\) là giao điểm của \(AE\) và \(BF\). LG a Chứng minh rằng \(OO’\) song song với hai mặt phẳng \((ADF)\) và \((BCE)\) Phương pháp giải: Sử dụng tính chất hình bình hành có giao điểm của hai đường chéo cắt nhau tại trung điểm mỗi đường. Sử dụng tính chất đường trung bình của tam giác. Sử dụng tính chất: Nếu đường thẳng \(d\) không nằm trong mặt phẳng \((\alpha)\) và \(d\) song song với đường thẳng \(d’\) nằm trong \((\alpha)\) thì \(d\) song song \((\alpha)\). Lời giải chi tiết:
Ta có tứ giác \(ABCD\) là hình bình hành, \(O=AC\cap BD\) nên \(O\) là trung điểm của \(AC, BD\). Tứ giác \(ABEF\) là hình bình hành, \(O’=AE\cap BF\) nên \(O’\) là trung điểm của \(AE, BF\) Xét tam giác \(BFD\) có \(O\) là trung điểm của \(BD\), \(O’\) là trung điểm của \(BF\) Theo tính chất đường trung bình của tam giác ta có \(OO’\parallel DF\) Mà \(DF\subset (ADF)\) \(\Rightarrow OO’\parallel (ADF)\) Xét tam giác \(ACE\) có \(O\) là trung điểm của \(AC\), \(O’\) là trung điểm của \(AE\) Theo tính chất đường trung bình của tam giác ta có \(OO’\parallel CE\) Mà \(CE\subset (BCE)\) \(\Rightarrow OO’\parallel (BCE)\). LG câu b Gọi \(M\) và \(N\) lần lượt là trọng tâm của các tam giác \(ABD\) và \(ABE\). Chứng minh rằng \(MN\parallel (CEF)\). Phương pháp giải: Sử dụng tính chất trọng tâm của tam giác. Sử dụng định lý Talet. Sử dụng tính chất: Nếu hai mặt phẳng lần lượt chứa hai đường thẳng song song thì giao tuyến của chúng (nếu có) cũng song song với hai đường thẳng đó hoặc trùng với một trong hai đường thẳng đó. Lời giải chi tiết: Gọi \(I\) là trung điểm \(AB\). Trong tam giác \(ABD\) có \(M\) là trọng tâm nên ta có \(\dfrac{IM}{ID}=\dfrac{1}{3}\). Trong tam giác \(ABE\) có \(N\) là trọng tâm nên ta có \(\dfrac{IN}{IE}=\dfrac{1}{3}\). Suy ra \(\dfrac{IM}{ID}=\dfrac{IN}{IE}=\dfrac{1}{3}\). Theo định lý Talet suy ra \(MN\parallel DE\text{(1)}\) Mà do tứ giác \(ABCD\) là hình bình hành nên \(AB\parallel = CD\) Và tứ giác \(ABEF\) là hình bình hành nên \(AB\parallel =EF\) Suy ra \(CD\parallel =EF\) \(\Rightarrow CEFD\) là hình bình hành \(DE\subset (CEF)\text{(2)}\) Từ \(\text{(1)}\) và \(\text{(2)}\) \(\Rightarrow MN\parallel (CEF)\). HocTot.Nam.Name.Vn
|