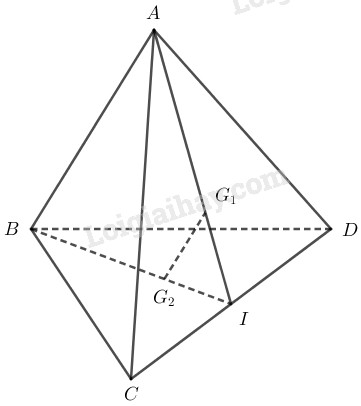
Bài 2.16 trang 71 SBT hình học 11

Đề bài

Cho tứ diện $ABCD$. Gọi $G_1$ và $G_2$ lần lượt là trọng tâm của tam giác $ACD$ và $BCD$. Chứng minh rằng $G_1G_2$ song song với các mặt phẳng $(ABC)$ và $(ABD)$.

Lời giải chi tiết

Gọi $I$ là trung điểm $CD$

Ta có $G_1$ là trọng tâm tam giác $ACD$ nên ta có $\dfrac{IG_1}{IA}=\dfrac{1}{3}$

Và $G_2$ là trọng tâm tam giác $BCD$ nên ta có $\dfrac{IG_2}{IB}=\dfrac{1}{3}$.

Khi đó $\dfrac{IG_1}{IA}=\dfrac{IG_2}{IB}=\dfrac{1}{3}$

Theo Talet ta được $G_1G_2\parallel AB$.

Do $\left\{ \begin{array}{l}{G_1}{G_2}\parallel AB\\AB \subset (ABC)\end{array} \right.$

$\Rightarrow G_1G_2\parallel (ABC)$.

Do $\left\{ \begin{array}{l}{G_1}{G_2}\parallel AB\\AB \subset (ABD)\end{array} \right.$

$\Rightarrow G_1G_2\parallel (ABD)$.

HocTot.Nam.Name.Vn