Bài 2.12 trang 67 SBT hình học 11Giải bài 2.12 trang 67 sách bài tập hình học 11. Cho tứ diện ABCD. Cho I và J tương ứng là trung điểm của BC và AC, M là một điểm tùy ý trên cạnh AD...
Lựa chọn câu để xem lời giải nhanh hơn
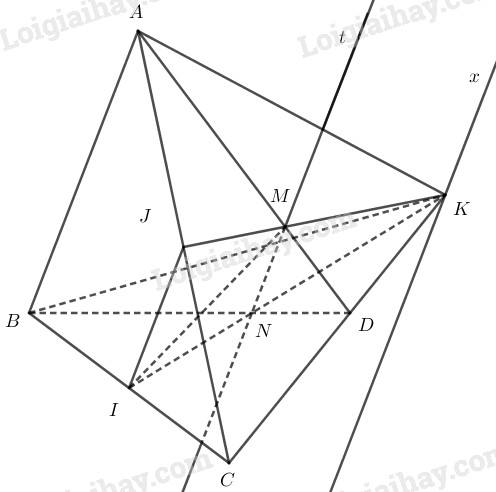
Cho tứ diện ABCD. Cho I và J tương ứng là trung điểm của BC và AC , M là một điểm tùy ý trên cạnh AD. LG a Tìm giao tuyến d của hai mặt phẳng (MIJ) và (ABD) Phương pháp giải: Cách tìm giao tuyến của hai mặt phẳng lần lượt chứa hai đường thẳng d và d′ song song với nhau: - Tìm điểm chung của hai mặt phẳng. - Giao tuyến của hai mặt phẳng là đường thẳng đi qua điểm chung và song song với d và d′. Lời giải chi tiết:
Ta có: M∈(MIJ) và M∈AD,AD⊂(ABD) ⇒M∈(ABD) ⇒M∈(MIJ)∩(ABD) Ta cũng có: {IJ∥ABIJ⊂(MIJ)AB⊂(ABD) ⇒(MIJ)∩(ABD)=d=Mt, Mt∥AB∥IJ. LG b Gọi N là giao điểm của BD với giao tuyến d, K là giao điểm của IN và JM. Tìm tập hợp điểm K khi M di động trên đoạn AD (M không là trung điểm của AD). Phương pháp giải: Từ K=IN∩JM của giả thiết ta suy ra được K là giao của hai mặt phẳng. Sử dụng tính chất “Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng sẽ có một đường thẳng chung đi qua điểm chung ấy” suy ra được K thuộc giao tuyến của hai mặt phẳng. Lời giải chi tiết: Trong (ABD) có Mt∥AB⇒Mt∩BD=N IN∩JM=K Khi đó K∈IN,IN⊂(BCD) ⇒K∈(BCD) và K∈JM,JM⊂(ACD) ⇒K∈(ACD) ⇒K∈(BCD)∩(ACD) Mặt khác (BCD)∩(ACD)=CD do đó K∈CD. Do vậy K nằm trên hai nửa đường thẳng Cm và Dn thuộc đường thẳng CD. (Để ý rằng nếu M là trung điểm của AD thì sẽ không có điểm K). LG c Tìm giao tuyến của hai mặt phẳng (ABK) và (MIJ) Phương pháp giải: Cách tìm giao tuyến của hai mặt phẳng lần lượt chứa hai đường thẳng d và d′ song song với nhau: - Tìm điểm chung của hai mặt phẳng. - Giao tuyến của hai mặt phẳng là đường thẳng đi qua điểm chung và song song với d và d′. Lời giải chi tiết: Ta có: {K∈(ABK)K∈IN,IN⊂(MIJ)⇒K∈(ABK)∩(MIJ) Mà {AB⊂(ABK)IJ⊂(MIJ)AB∥IJ⇒(ABK)∩(MIJ)=Kx, Kx∥AB∥IJ. HocTot.Nam.Name.Vn
>> 2K9 Học trực tuyến - Định hướng luyện thi TN THPT, ĐGNL, ĐGTD ngay từ lớp 11 (Xem ngay) cùng thầy cô giáo giỏi trên Tuyensinh247.com. Bứt phá điểm 9,10 chỉ sau 3 tháng, tiếp cận sớm các kì thi.
|