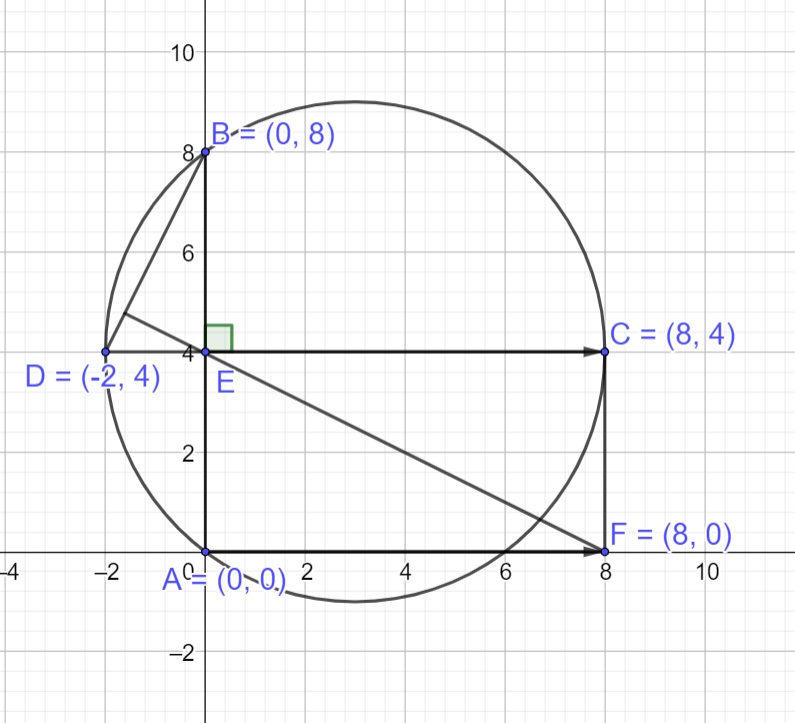
Giải bài 2 trang 73 SGK Toán 10 tập 2 – Chân trời sáng tạoCho AB và CD là hai dây cung vuông góc tại E của đường tròn (O) .Vẽ hình chữ nhật AECF. Dùng phương pháp tọa độ mặt phẳng để chứng minh EF vuông góc với DB Tổng hợp đề thi học kì 2 lớp 10 tất cả các môn - Chân trời sáng tạo Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa... Đề bài Cho AB và CD là hai dây cung vuông góc tại E của đường tròn (O) .Vẽ hình chữ nhật AECF. Dùng phương pháp tọa độ mặt phẳng để chứng minh EF vuông góc với DB Phương pháp giải - Xem chi tiết Bước 1: Xét với đường tròn bất kì, cho tọa độ các điểm A, B, C, D Bước 2: Xác định tọa độ điểm E, F Bước 3: Tính →EF.→DB, suy ra vuông góc Lời giải chi tiết Xét với đường tròn (O) có phương trình (O):(x−3)2+(y−4)2=25 Cho các điểm A(0;0),B(0;8),C(8;4),D(−2;4) nằm trên đường tròn (O) và thỏa mãn AB vuông góc với CD
Phương trình đường thẳng đi qua hai điểm A, B có dạng x=0 Phương trình đường thẳng đi qua hai điểm C, D có dạng y=4 Ta có AB vuông góc với CD tại điểm E nên tọa độ điểm E là nghiệm của hệ sau: {x=0y=4⇔E(0;4) Gọi tọa độ của điểm F là: F(x;y) ACEF là hình chữ nhật nên →AF=→EC, mặt khác ta có: →AF=(x;y),→EC=(8;0) Suy ra tọa độ điểm F là: F(8;0) →EF=(8;−4),→DB=(2;4)⇒→EF.→BD=8.2+(−4).4=0⇒→EF⊥→BD Vậy ta chứng minh được EF vuông góc với DB
|