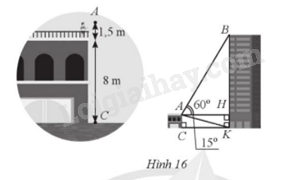
Giải bài 17 trang 85 sách bài tập toán 9 - Cánh diều tập 1Bạn Đức đứng trên nóc ngôi nhà ở độ cao 8 m. Vị trí mắt bạn Đức (tại vị trí A) cách nóc nhà 1,5 m. Bạn nhìn thấy vị trí B cao nhất của một toà nhà với góc tạo bởi tia AB và tia AH theo phương nằm ngang là \(\widehat {BAH} = 60^\circ \). Bạn Đức cũng nhìn thấy vị trí K tại chân tòa nhà đó với góc tạo bởi tia AK và tia AH là \(\widehat {HAK} = 15^\circ \), AH vuông góc với BK tại H (Hình 16). Tính chiều cao BK của tòa nhà (làm tròn kết quả đến hàng phần mười của mét). Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn - Cánh diều Toán - Văn - Anh - KHTN - Lịch sử và Địa lí Đề bài Bạn Đức đứng trên nóc ngôi nhà ở độ cao 8 m. Vị trí mắt bạn Đức (tại vị trí A) cách nóc nhà 1,5 m. Bạn nhìn thấy vị trí B cao nhất của một toà nhà với góc tạo bởi tia AB và tia AH theo phương nằm ngang là \(\widehat {BAH} = 60^\circ \). Bạn Đức cũng nhìn thấy vị trí K tại chân tòa nhà đó với góc tạo bởi tia AK và tia AH là \(\widehat {HAK} = 15^\circ \), AH vuông góc với BK tại H (Hình 16). Tính chiều cao BK của tòa nhà (làm tròn kết quả đến hàng phần mười của mét).
Phương pháp giải - Xem chi tiết Bước 1: Tính HK. Bước 2: Tính AH dựa vào hệ thức lượng trong tam giác vuông AHK. Bước 3: Tính BH dựa vào hệ thức lượng trong tam giác vuông AHB. Bước 4: Chiều cao của tòa nhà là BK = HK + BH. Lời giải chi tiết Xét CAHK có \(\widehat {ACK} = \widehat {CKH} = \widehat {KHA} = 90^\circ \) nên CAHK là hình chữ nhật. Suy ra \(HK = CA = 8 + 1,5 = 9,5\)m. Xét tam giác vuông AHK có \(\tan \widehat {HAK} = \frac{{HK}}{{AH}}\) do đó \(AH = \frac{{HK}}{{\tan \widehat {HAK}}} = \frac{{9,5}}{{\tan 15^\circ }}\). Xét tam giác vuông AHB có \(\tan \widehat {HAB} = \frac{{HB}}{{AH}}\) do đó \(BH = \tan \widehat {HAB}.AH = \tan 60^\circ .\frac{{9,5}}{{\tan 15^\circ }}.\) Chiều cao của tòa nhà là: \(BK = HK + BH = 9,5 + \tan 60^\circ .\frac{{9,5}}{{\tan 15^\circ }} \approx 70,9m.\)  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
>> Học trực tuyến Lớp 9 & Lộ trình UP10 trên Tuyensinh247.com >> Chi tiết khoá học xem: TẠI ĐÂY Đầy đủ khoá học các bộ sách (Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều), theo lộ trình 3: Nền Tảng, Luyện Thi, Luyện Đề. Bứt phá điểm lớp 9, thi vào lớp 10 kết quả cao. Hoàn trả học phí nếu học không hiệu quả.
|
