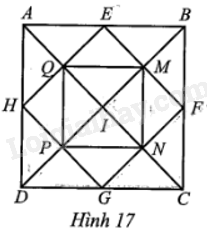
Giải bài 17 trang 112 sách bài tập toán 9 - Cánh diều tập 2Cho hình vuông ABCD, I là giao điểm của hai đường chéo AC, BD. E, F, G, H lần lượt là trung điểm các cạnh AB, BC, CD, DA. Q, N lần lượt là giao điểm của AC với HE và AC với GF; M, P lần lượt là giao điểm của BD với EF và BD với GH (Hình 17). Phép quay thuận chiều 90° tâm I có giữ nguyên các tứ giác EFGH và tứ giác MNPQ hay không? Vì sao? Đề bài Cho hình vuông ABCD, I là giao điểm của hai đường chéo AC, BD. E, F, G, H lần lượt là trung điểm các cạnh AB, BC, CD, DA. Q, N lần lượt là giao điểm của AC với HE và AC với GF; M, P lần lượt là giao điểm của BD với EF và BD với GH (Hình 17). Phép quay thuận chiều 90° tâm I có giữ nguyên các tứ giác EFGH và tứ giác MNPQ hay không? Vì sao?
Phương pháp giải - Xem chi tiết Dựa vào phép quay thuận chiều \({\alpha ^o}\) (\({0^o} < {\alpha ^o} < {360^o}\)) tâm O giữ nguyên điểm O, biến điểm M (khác điểm O) thành điểm M’ thuộc đường tròn (O; OM) sao cho tia OM quay thuận chiều kim đồng hồ đến tia OM’ thì điểm M tạo nên cung MnM’ có số đo \({\alpha ^o}\). Dựa vào phép quay thuận chiều \({\alpha ^o}\) (\({0^o} < {\alpha ^o} < {360^o}\)) tâm O được phát biểu tương tự như trên. Lời giải chi tiết Vì I là giao điểm của hai đường chéo AC, BD của hình vuông ABCD nên I là trung điểm của AC và BD. Vì E, I lần lượt là trung điểm các cạnh AB, AC nên EI là đường trung bình của ∆ABC. Suy ra EI // BC và \(EI = \frac{1}{2}BC\). Chứng minh tương tự, ta cũng có IG là đường trung bình của ∆BCD. Suy ra IG // BC và \(IG = \frac{1}{2}BC\). Do đó IE // BC // IG và IE = IG. Theo tiên đề Euclid, qua I có hai đường thẳng IE và IG cùng song song với BC nên ba điểm E, I, G thẳng hàng. Lại có IE = IG nên I là trung điểm của EG. Chứng minh tương tự ta cũng có I là trung điểm của HF. Do đó tứ giác EFGH là hình bình hành. Ta có I là trung điểm của EG và HF nên EG = 2EI và HF = 2IF. Mà BC = 2EI, CD = 2IF và BC = CD (do ABCD là hình vuông) nên EG = HF. Do đó hình bình hành EFGH là hình chữ nhật. Mặt khác, IE // BC, IF // CD và BC ⊥ CD nên IE ⊥ IF hay EG ⊥ HF. Suy ra hình chữ nhật EFGH là hình vuông và I là giao điểm hai đường chéo. Như vậy, phép quay thuận chiều 90° tâm I giữ nguyên hình vuông EFGH. ⦁ Ta có E, F lần lượt là trung điểm của AB, BC nên EF là đường trung bình của tam giác, do đó EF // AC hay EM // AI. Xét ∆ABI có E là trung điểm của AB và EM // AI nên EM là đường trung bình của tam giác, do đó M là trung điểm của BI, nên \(MI = \frac{1}{2}BI\) mà IB = ID = \(\frac{1}{2}BD\). Nên \(IM = \frac{1}{4}BD\). Chứng minh tương tự ta có IM = IP = \(\frac{1}{4}BD\); IN = IQ = \(\frac{1}{4}AC\). Mà AC = BD nên IM = IN = IP = IQ và MP = NQ. Do đó MNPQ là hình chữ nhật, lại có MP ⊥ NQ (do AC ⊥ BD) nên hình chữ nhật MNPQ là hình vuông có I là giao điểm hai đường chéo. Như vậy, phép quay thuận chiều 90° tâm I giữ nguyên hình vuông MNPQ. Vậy phép quay thuận chiều 90° tâm I giữ nguyên các tứ giác EFGH và MNPQ.  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
