Bài 16 trang 81 SBT toán 8 tập 1Giải bài 16 trang 81 sách bài tập toán 8. Chứng minh rằng trong hình thang các tia phân giác của hai góc kề một cạnh bên vuông góc với nhau. Đề bài Chứng minh rằng trong hình thang các tia phân giác của hai góc kề một cạnh bên vuông góc với nhau. Phương pháp giải - Xem chi tiết Ta sử dụng kiến thức: +) Hai góc kề một cạnh bên của hình thang bằng \(180^0.\) +) Tổng ba góc trong một tam giác bằng \(180^0.\) Lời giải chi tiết
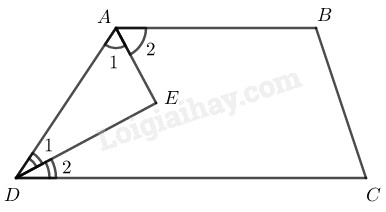
Giải sử hình thang \(ABCD\) có \(AB// CD\) Suy ra \(\widehat A + \widehat D = {180^0}\) (hai góc trong cùng phía bù nhau) Ta có: \(\displaystyle {\widehat A_1} = {\widehat A_2} = {1 \over 2}\widehat A\) (vì AE là tia phân giác của góc A) \( \displaystyle {\widehat D_1} = {\widehat D_2} = {1 \over 2}\widehat D \) (vì DE là tia phân giác của góc D) Suy ra: \({\widehat A_1} + {\widehat D_1} = \displaystyle {1 \over 2}(\widehat A + \widehat D )\)\(=\displaystyle{1 \over 2}.180^0= {90^0}\) Trong \(∆ AED\) ta có : \(\widehat {AED} + {\widehat A_1} + {\widehat D_1} = {180^0}\) (tổng ba góc trong tam giác) \( \Rightarrow \widehat {AED} = {180^0} - \left( {{{\widehat A}_1} + {{\widehat D}_1}} \right) \)\(= {180^0} - {90^0} = {90^0}\) Vậy \(AE ⊥ DE\) HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
|
