Bài 17 trang 81 SBT toán 8 tập 1Giải bài 17 trang 81 sách bài tập toán 8. Cho tam giác ABC . Các tia phân giác của các góc B và C cắt nhau ở I. Qua I kẻ đường thẳng song song với BC, cắt các cạnh AB và AC ở D và E...
Lựa chọn câu để xem lời giải nhanh hơn
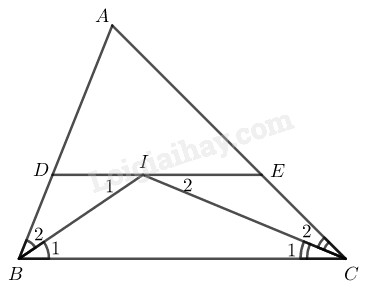
Cho tam giác \(ABC.\) Các tia phân giác của các góc \(B\) và \(C\) cắt nhau ở \(I.\) Qua \(I\) kẻ đường thẳng song song với \(BC,\) cắt các cạnh \(AB\) và \(AC\) ở \(D\) và \(E.\) LG a Tìm các hình thang trong hình vẽ. Phương pháp giải: Sử dụng định nghĩa: Hình thang là tứ giác có hai cạnh đối song song. Lời giải chi tiết:
Đường thẳng đi qua \(I\) song song với \(BC\) cắt \(AB\) tại \(D\) và \(AC\) tại \(E,\) ta có các hình thang sau: \(BDEC,\) \(BDIC,\) \(BIEC.\) LG b Chứng minh rằng hình thang \(BDEC\) có một cạnh đáy bằng tổng hai cạnh bên. Phương pháp giải: Sử dụng tính chất hai góc so le trong, tam giác cân. Lời giải chi tiết: \(\) \(DE // BC\) (theo cách vẽ) \( \Rightarrow {\widehat I_1} = {\widehat B_1}\) (hai góc so le trong) Mà \({\widehat B_1} = {\widehat B_2}\) (vì BI là phân giác góc B) Suy ra: \({\widehat I_1} = {\widehat B_2}\) Do đó: \(∆ BDI\) cân tại \(D\) \(⇒ DI = DB \;\;\; (1)\) Ta có: \({\widehat I_2} = {\widehat C_1}\) (so le trong) \({\widehat C_1} = {\widehat C_2}\) (vì CI là phân giác góc C) Suy ra: \({\widehat I_2} = {\widehat C_2}\) do đó: \(∆ CEI\) cân tại \(E\) \(⇒ IE = EC \;\;\; \;\;\; (2)\) \(DE = DI + IE \;\;\; (3)\) Từ \((1),\)\( (2)\) và \((3)\) suy ra: \(DE = BD + CE\) HocTot.Nam.Name.Vn
|