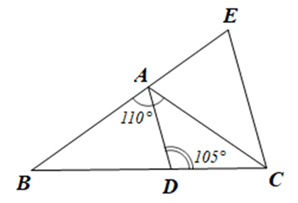
Giải Bài 16 trang 71 sách bài tập toán 7 - Cánh diềuCho tam giác ABC có \(\widehat {A{}^{}} = {110^o}\) và \(\widehat B = \widehat C\) . Trên cạnh BC lấy điểm D sao cho \(\widehat {A{\rm{D}}C} = {105^o}\). Từ C kẻ đường thẳng song song với AD cắt tia BA tại E. Chứng minh: a) AE < CE; Tổng hợp đề thi học kì 2 lớp 7 tất cả các môn - Cánh diều Toán - Văn - Anh - Khoa học tự nhiên... Đề bài Cho tam giác ABC có \(\widehat {A{}^{}} = {110^o}\) và \(\widehat B = \widehat C\) . Trên cạnh BC lấy điểm D sao cho \(\widehat {A{\rm{D}}C} = {105^o}\). Từ C kẻ đường thẳng song song với AD cắt tia BA tại E. Chứng minh: a) AE < CE; b) EC < BC < BE. Phương pháp giải - Xem chi tiết - Áp dụng quan hệ giữa góc và cạnh đối diện trong tam giác ACE để chúng minh AE < CE. - Áp dụng mối quan hệ giữa góc và cạnh đối diện trong tam giác BEC để chứng minh EC < BC < BE. Lời giải chi tiết •Xét ∆ACB có: \(\widehat {BAC} + \widehat {BCA} + \hat B = 180^\circ \) (tổng ba góc của một tam giác) Mà \(\widehat {BAC} = 110^\circ ,\)\(\widehat B = \widehat {ACB}\) (giả thiết) Suy ra \(\hat B = \widehat {ACB} = \frac{{180^\circ - \widehat {BAC}}}{2} = \frac{{180^\circ - 110^\circ }}{2} = 35^\circ \) •Ta có \(\widehat {BAC} + \widehat {CAE} = 180^\circ \) (hai góc kề bù) Suy ra \(\widehat {CAE} = 180^\circ - \widehat {BAC} = 180^\circ - 110^\circ = 70^\circ \) . • Do AD // EC (giả thiết) nên \(\widehat {ADC} + \widehat {ECD} = {180^o}\) (hai góc trong cùng phía). Suy ra \(\widehat {ECD} = {180^o} - \widehat {ADC} = {180^o} - {105^o} = {75^o}.\) Lại có \(\widehat {ACB} + \widehat {ACE} = \widehat {ECD}\) (hai góc kề nhau) Do đó \(\widehat {ACE} = \widehat {ECD} - \widehat {ACB} = 75^\circ - {35^o} = 40^\circ .\) • Trong ∆ACE có: \(\widehat {ACE} < \widehat {CAE}\) (do 40° < 70°) Do đó AE < CE (trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn). Vậy AE < CE. b) Xét ∆EBC có: \(\hat E + \widehat {BCE} + \hat B = 180^\circ \) (tổng ba góc của một tam giác) Mà \(\widehat {BCE} = 75^\circ ,\hat B = 35^\circ \) Suy ra \(\hat E = 180^\circ - \hat B - \widehat {BCE} = 180^\circ - 35^\circ - 75^\circ = 70^\circ \) Trong tam giác BCE có: \(\hat B < \hat E < \widehat {BCE}\) (do 35° < 70° < 75°). Nên EC < BC < BE (trong một tam giác, cạnh đối diện với góc lớn hơn là cạnh lớn hơn). Vậy EC < BC < BE.
|