Bài 1.6 trang 13 SBT đại số và giải tích 11

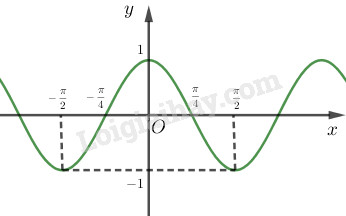
LG a

Chứng minh rằng $\cos 2\left( {x + k\pi } \right) = \cos 2x,k \in Z$. Từ đó vẽ đồ thị hàm số $y = \cos 2x$

Phương pháp giải:

Sử dụng công thức $\cos (\alpha  + k2\pi ) = \cos \alpha$

Lời giải chi tiết:

$\cos 2(x + k\pi ) = \cos (2x + k2\pi )$ $= \cos 2x,k \in Z$

Vậy hàm số $y = \cos 2x$ là hàm số chẵn, tuần hoàn, có chu kỳ $\pi$.

Đồ thị hàm số đi qua các điểm $\left( {0;1} \right),\left( { - \dfrac{\pi }{4};0} \right),$ $\left( {\dfrac{\pi }{4};0} \right),\left( { - \dfrac{\pi }{2}; - 1} \right),\left( {\dfrac{\pi }{2};1} \right)$

Quảng cáo

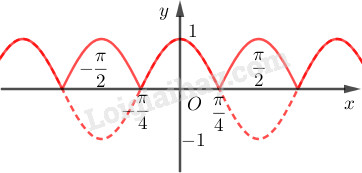
LG b

Từ đồ thị hàm số $y = \cos 2x$ , hãy vẽ đồ thị hàm số $y = \left| {\cos 2x} \right|$

Phương pháp giải:

Cách dựng đồ thị hàm số $y = \left| {f(x)} \right|$ từ đồ thị hàm số $y = f(x)$:

+ Giữ nguyên phần đồ thị phía trên trục $Ox$ của đồ thị hàm số $y = f(x)$

+ Lấy đối xứng phần đồ thị phía dưới trục $Ox$ của đồ thị $y = f(x)$ qua $Ox$

+ Xóa phần đồ thị phía dưới trục $Ox$ của đồ thị hàm số $y = f(x)$.

Lời giải chi tiết:

Đồ thị hàm số $y = \left| {\cos 2x} \right|$ gồm:

+ Phần đồ thị phía trên trục $Ox$ của đồ thị hàm số $y = \cos 2x$

+ Phần đồ thị có được từ việc lấy đối xứng phần đồ thị phía dưới trục $Ox$ của đồ thị hàm số $y = \cos 2x$.

Đồ thị hàm số $y = \left| {\cos 2x} \right|$ là:

HocTot.Nam.Name.Vn