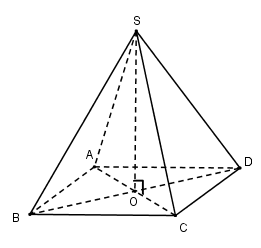
Bài 1.46 trang 22 SBT hình học 12Giải bài 1.46 trang 22 sách bài tập hình học 12. Cho (H) là khối chóp tứ giác đều có tất cả các cạnh bằng a... Đề bài Cho \(\left( H \right)\) là khối chóp tứ giác đều có tất cả các cạnh bằng \(a\). Thể tích của \(\left( H \right)\) là: A. \(\dfrac{{{a^3}}}{3}\) B. \(\dfrac{{{a^3}\sqrt 2 }}{6}\) C. \(\dfrac{{{a^3}\sqrt 3 }}{4}\) D. \(\dfrac{{{a^3}\sqrt 3 }}{2}\) Phương pháp giải - Xem chi tiết - Tính diện tích đáy và chiều cao khối chóp. - Tính thể tích theo công thức \(V = \dfrac{1}{3}Sh\). Lời giải chi tiết
Gọi \(O = AC \cap BD\) Vì chóp \(S.ABCD\) đều nên \(SO \bot \left( {ABCD} \right)\) Ta có: \(AC = BD = a\sqrt 2 \)\( \Rightarrow OA = \dfrac{1}{2}AC = \dfrac{{a\sqrt 2 }}{2}\) \(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OA\) \( \Rightarrow \Delta SOA\) vuông tại \(O\) \( \Rightarrow SO = \sqrt {S{A^2} - O{A^2}} \) \( = \sqrt {{a^2} - \dfrac{{{a^2}}}{2}} = \dfrac{{a\sqrt 2 }}{2}\) Vậy \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}}\)\( = \dfrac{1}{3}\dfrac{{a\sqrt 2 }}{2}{a^2} = \dfrac{{{a^3}\sqrt 2 }}{6}\) Chọn B. HocTot.Nam.Name.Vn  Chia sẻ Bình luận
|
