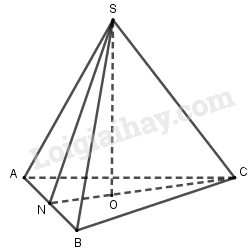
Bài 1.51 trang 23 SBT hình học 12

Đề bài

Cho hình chóp tam giác đều \(S.ABC\) có cạnh đáy bằng \(a\), diện tích một mặt bên bằng \(\dfrac{{5\sqrt 3 {a^2}}}{{12}}\). Thể tích của hình chóp bằng:

A. \(\dfrac{{\sqrt 6 }}{{24}}{a^3}\)                  B. \(\dfrac{{\sqrt 6 }}{{12}}{a^3}\)

C. \(\dfrac{{\sqrt 6 }}{4}{a^3}\)                  D. \(\dfrac{{\sqrt 2 }}{{12}}{a^3}\)

Lời giải chi tiết

Tam giác \(ABC\) đều có \({S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\) và \(CN = \dfrac{{a\sqrt 3 }}{2}\) \( \Rightarrow ON = \dfrac{1}{3}CN = \dfrac{{a\sqrt 3 }}{6}\).

Tam giác \(SAB\) có \({S_{SAB}} = \dfrac{1}{2}AB.SN\) \( \Rightarrow SN = \dfrac{{2{S_{SAB}}}}{{AB}} = \dfrac{{2.\dfrac{{5\sqrt 3 {a^2}}}{{12}}}}{a} = \dfrac{{5\sqrt 3 a}}{6}\).

Tam giác \(SON\) vuông tại \(O\) có \(SO = \sqrt {S{N^2} - O{N^2}} \) \( = \sqrt {\dfrac{{75{a^2}}}{{36}} - \dfrac{{3{a^2}}}{{36}}}  = a\sqrt 2 \)

Vậy thể tích khối chóp \({V_{S.ABC}} = \dfrac{1}{3}SO.{S_{ABC}}\) \( = \dfrac{1}{3}.a\sqrt 2 .\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt 6 }}{{12}}\).

Chọn B.

HocTot.Nam.Name.Vn