Giải bài 1.44 trang 31 sách bài tập toán 12 - Kết nối tri thứcMột hòn đảo nhỏ cách điểm P trên bờ biển khoảng (3) km, một thị trấn ở điểm A cách điểm P (12) km (xem hình vẽ). Nếu một người trên đảo chèo thuyền với vận tốc (2,5) km/h và đi bộ với vận tốc (4) km/h thì thuyền nên neo đậu ở vị trí nào trên đoạn PA để người đó đến thị trấn trong thời gian ngắn nhất? Tổng hợp đề thi học kì 1 lớp 12 tất cả các môn - Kết nối tri thức Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa Đề bài Một hòn đảo nhỏ cách điểm P trên bờ biển khoảng \(3\) km, một thị trấn ở điểm A cách điểm P \(12\) km (xem hình vẽ). Nếu một người trên đảo chèo thuyền với vận tốc \(2,5\) km/h và đi bộ với vận tốc \(4\) km/h thì thuyền nên neo đậu ở vị trí nào trên đoạn PA để người đó đến thị trấn trong thời gian ngắn nhất?
Phương pháp giải - Xem chi tiết + Đặt ẩn và điều kiện cho ẩn biểu diễn khoảng cách từ A đến vị trí thuyền neo đậu trên đoạn PA. + Biểu diễn tổng quãng đường mà người đó phải di chuyển theo x từ đó biểu diễn tổng thời gian. + Tìm giá trị nhỏ nhất của tổng thời gian đó (đưa về bài toán tìm giá trị nhỏ nhất trên đoạn đã học). Lời giải chi tiết
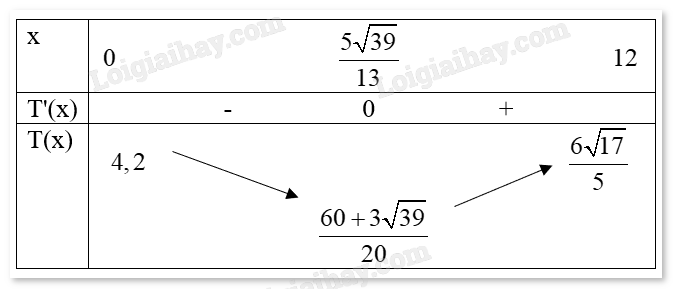
Gọi vị trí hòn đảo là B và vị trí thuyền neo đậu trên bờ là C. Ta cần tìm vị trí điểm C trên đoạn PA sao cho thời gian thuyền đi từ đảo vào bờ (đoạn BC) và đi bộ tiếp từ C đến thị trấn A (đoạn CA) là ngắn nhất. Gọi đoạn PC = x (km) với \(0 \le x \le 12\). Áp dụng định lý Pythagore trong tam giác BPC vuông tại P có: \(BC = \sqrt {{x^2} + 9} \) (km). Thuyền đi với vận tốc 2,5 km/h nên thời gian đi hết đoạn BC là \(\frac{{\sqrt {{x^2} + 9} }}{{2,5}}\) (giờ). Ta có: AC = PA – x = 12 – x (km). Người đi bộ với vận tốc 4 km/h nên thời gian đi hết đoạn AC là \(\frac{{12 - x}}{4}\) (giờ). Tổng thời gian người đó đi từ đảo đến thị trấn A là: \(T(x) = \frac{{\sqrt {{x^2} + 9} }}{{2,5}} + \frac{{12 - x}}{4}\) (giờ). Bài toán trở thành tìm giá trị nhỏ nhất của hàm T(x) trên đoạn [0;12]. Ta có: \(T'(x) = \frac{{2x}}{{5\sqrt {{x^2} + 9} }} - \frac{1}{4}\). \(T'(x) = 0 \Leftrightarrow \frac{{2x}}{{5\sqrt {{x^2} + 9} }} - \frac{1}{4} = 0 \Leftrightarrow 8x = 5\sqrt {{x^2} + 9} \). Giải phương trình trên ta được \(x = \frac{{5\sqrt {39} }}{{13}} \approx 2,4\) là giá trị thỏa mãn điều kiện. Bảng biến thiên:
Vậy điểm neo đậu thuyền trên đoạn PA cách P khoảng 2,4 km để thời gian di chuyển là ngắn nhất.
|