Giải bài 14 trang 111 sách bài tập toán 9 - Cánh diều tập 2a) Cho hình bình hành ABCD, O là giao điểm của hai đường chéo AC và BD. Chỉ ra phép quay ngược chiều tâm O sao cho phép quay đó biến mỗi điểm C và D thành điểm đối xứng với nó qua tâm O. b) Cho lục giác đều A1A2A3A4A5A6 tâm O. Chỉ ra phép quay thuận chiều tâm O sao cho phép quay đó biến mỗi điểm A3, A4, A5 thành điểm đối xứng với nó qua tâm O. Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn - Cánh diều Toán - Văn - Anh - KHTN - Lịch sử và Địa lí Đề bài a) Cho hình bình hành ABCD, O là giao điểm của hai đường chéo AC và BD. Chỉ ra phép quay ngược chiều tâm O sao cho phép quay đó biến mỗi điểm C và D thành điểm đối xứng với nó qua tâm O. b) Cho lục giác đều A1A2A3A4A5A6 tâm O. Chỉ ra phép quay thuận chiều tâm O sao cho phép quay đó biến mỗi điểm A3, A4, A5 thành điểm đối xứng với nó qua tâm O. Phương pháp giải - Xem chi tiết Dựa vào phép quay thuận chiều \({\alpha ^o}\) (\({0^o} < {\alpha ^o} < {360^o}\)) tâm O giữ nguyên điểm O, biến điểm M (khác điểm O) thành điểm M’ thuộc đường tròn (O; OM) sao cho tia OM quay thuận chiều kim đồng hồ đến tia OM’ thì điểm M tạo nên cung MnM’ có số đo \({\alpha ^o}\). Dựa vào phép quay thuận chiều \({\alpha ^o}\) (\({0^o} < {\alpha ^o} < {360^o}\)) tâm O được phát biểu tương tự như trên. Lời giải chi tiết a)
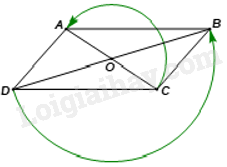
Vì ABCD là hình bình hành nên O là trung điểm của hai đường chéo AC và BD. Do đó A, B lần lượt là điểm đối xứng với C, D qua điểm O. Ta có OA = OC và \(\widehat {COA} = {180^o}\)nên tia OC quay đến tia OA ngược chiều kim đồng hồ tạo thành một cung có số đo bằng 180°. Như vậy, phép quay ngược chiều 180° tâm O biến điểm C thành điểm A đối xứng với nó qua tâm O. Tương tự, ta có OB = OD và \(\widehat {DOB} = {180^o}\)nên phép quay ngược chiều 180° tâm O biến điểm D thành điểm B đối xứng với nó qua tâm O. b)
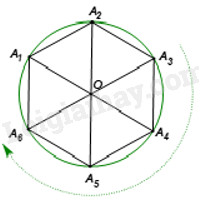
Vì A1A2A3A4A5A6 là hình lục giác đều nên O là trung điểm của ba đường chéo A1A4, A2A5 và A3A6. Do đó A6, A1, A2 lần lượt là điểm đối xứng với A3, A4, A5 qua điểm O. Ta có OA6 = OA3 và \(\widehat {{A_3}O{A_6}} = {180^o}\) nên tia OA3 quay đến tia OA6 thuận chiều kim đồng hồ tạo thành một cung có số đo bằng 180°. Như vậy, phép quay thuận chiều 180° tâm O biến điểm A3 thành điểm A6 đối xứng với nó qua tâm O. Tương tự, ta chứng minh được phép quay thuận chiều 180° tâm O biến mỗi điểm A4, A5 lần lượt thành điểm A1, A2 đối xứng với mỗi điểm qua tâm O.
|