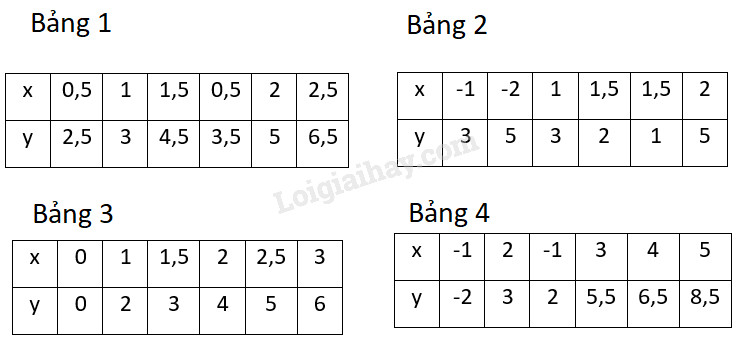
Bài 1.1 phần bài tập bổ sung trang 61 SBT toán 9 tập 1Giải bài 1.1 phần bài tập bổ sung trang 61 sách bài tập toán 9. Cho 4 bảng ghi các giá trị tương ứng của x và y.. Đề bài Cho 4 bảng ghi các giá trị tương ứng của \(x\) và \(y\) (h. bs. 1)
Trong các bảng trên đây, bảng xác định \(y\) là hàm số của \(x\) là: (A) Bảng 1; (B) Bảng 2; (C) Bảng 3; (D) Bảng 4. Phương pháp giải - Xem chi tiết - Nếu đại lượng \(y\) phụ thuộc vào đại lượng thay đổi \(x\) sao cho với mỗi giá trị \(x\) ta luôn xác định được chỉ một giá trị tương ứng của \(y\) thì \(y\) được gọi là hàm số của \(x\), \(x\) được gọi là biến số. - Hàm số có thể cho bằng bảng hoặc bằng công thức. - Giá trị của \(f(x)\) tại \({x_0}\) kí hiệu là \(f({x_0}).\) Lời giải chi tiết Áp dụng định nghĩa của hàm số thì đáp án (C) đúng. Đáp án A sai vì với \(x=0,5\) có 2 giá trị của \(y\) là \(y=2,5\) và \(y=3,5\) Đáp án B sai vì với \(x=1,5\) có 2 giá trị của \(y\) là \(y=2\) và \(y=1\) Đáp án D sai vì với \(x=-1\) có 2 giá trị của \(y\) là \(y=2\) và \(y=-2\) HocTot.Nam.Name.Vn  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
