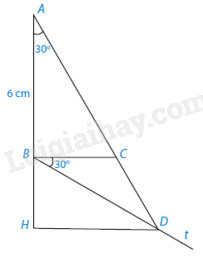
Giải bài 10 trang 135 vở thực hành Toán 9 tập 2Cho tam giác ABC vuông tại B, góc (widehat A = {30^o},AB = 6cm). Vẽ tia Bt sao cho (widehat {tBC} = {30^o}), cắt tia AC ở D (C nằm giữa A và D). a) Chứng minh tam giác ABD cân tại B. b) Tính khoảng cách từ D đến đường thẳng AB. Đề bài Cho tam giác ABC vuông tại B, góc \(\widehat A = {30^o},AB = 6cm\). Vẽ tia Bt sao cho \(\widehat {tBC} = {30^o}\), cắt tia AC ở D (C nằm giữa A và D). a) Chứng minh tam giác ABD cân tại B. b) Tính khoảng cách từ D đến đường thẳng AB. Phương pháp giải - Xem chi tiết a) + Sử dụng tính chất tổng ba góc trong một tam giác vào tam giác ABD, tính được góc ADB. + Suy ra \(\widehat {ADB} = \widehat {BAD}\) nên \(\Delta \)ABD cân tại B. b) + Ta có: \(AC = \frac{{AB}}{{\cos A}},BC = AB.\tan A\) nên tính được AC, BC. + Chứng minh được \(BC = CD\) nên tính được CD. + Kẻ DH vuông góc với AB tại H, có \(DH = AD.\sin \widehat {DAB} = \left( {AC + CD} \right)\sin \widehat {DAB}\) nên tính được DH. Lời giải chi tiết
a) Ta có: \(\widehat {BAD} + \widehat {BDA} + \widehat {ADB} = {180^o}\) (Tổng ba góc trong một tam giác). Suy ra \(\widehat {ADB} = {180^0} - \widehat {BAD} - \widehat {ABC} - \widehat {CBD}\)\( = {180^0} - {30^0} - {90^0} - {30^0} = {30^0}\) Vậy \(\widehat {ADB} = \widehat {BAD}\) nên \(\Delta \)ABD là tam giác cân tại B. b) Ta có: \(AC = \frac{{AB}}{{\cos A}} = \frac{6}{{\cos {{30}^o}}} = 4\sqrt 3 \left( {cm} \right)\). \(BC = AB.\tan {30^o} = 6.\frac{{\sqrt 3 }}{3} = 2\sqrt 3 \left( {cm} \right)\). Lại có: \(BC = CD\) do \(\widehat {CBD} = \widehat {CDB}\) (đều bằng \({30^o}\)) nên \(CD = 2\sqrt 3 \left( {cm} \right)\). Kẻ DH vuông góc với AB tại H. Ta có: \(DH = AD.\sin \widehat {DAB} = \left( {AC + CD} \right)\sin \widehat {DAB} \\= \left( {4\sqrt 3 + 2\sqrt 3 } \right).\sin {30^o} = 3\sqrt 3 \left( {cm} \right).\)  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
