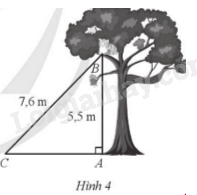
Giải bài 1 trang 81 sách bài tập toán 9 - Cánh diều tập 1Hình 4 mô tả một con mèo bị mắc kẹt ở vị trí B trên cảnh cây với độ cao AB = 5,5 m. Để đưa con mèo xuống, người ta cần phải đặt thang dựa vào cành cây đó. Khoảng cách từ chân thang đến điểm chạm vào cảnh cây là BC = 7,6 m. Góc giữa thang với phương nằm ngang là góc BCA. Tính các tỉ số lượng giác của góc BCA (làm tròn kết quả đến hàng phần trăm). Đề bài Hình 4 mô tả một con mèo bị mắc kẹt ở vị trí B trên cảnh cây với độ cao AB = 5,5 m. Để đưa con mèo xuống, người ta cần phải đặt thang dựa vào cành cây đó. Khoảng cách từ chân thang đến điểm chạm vào cảnh cây là BC = 7,6 m. Góc giữa thang với phương nằm ngang là góc BCA. Tính các tỉ số lượng giác của góc BCA (làm tròn kết quả đến hàng phần trăm).
Phương pháp giải - Xem chi tiết Bước 1: Áp dụng định lý Pythagore để tính AC. Bước 2: Dùng các công thức lượng giác để tính các tỉ số lượng giác của góc BCA. Lời giải chi tiết Xét tam giác ABC vuông tại A, ta có: \(AC = \sqrt {B{C^2} - A{B^2}} \) (Định lý Pythagore) \(AC = \sqrt {7,{6^2} - 5,{5^2}} = \sqrt {27,51} \left( m \right)\). \(\sin \widehat {BCA} = \frac{{AB}}{{CB}} = \frac{{5,5}}{{7,6}} = \frac{{55}}{{76}} \approx 0,72\); \(\cos \widehat {BCA} = \frac{{CA}}{{CB}} = \frac{{\sqrt {27,51} }}{{7,6}} \approx 0,69\); \(\tan \widehat {BCA} = \frac{{AB}}{{AC}} = \frac{{5,5}}{{\sqrt {27,51} }} \approx 1,05\); \(\cot \widehat {BCA} = \frac{{AC}}{{AB}} = \frac{{\sqrt {27,51} }}{{5,5}} \approx 0,95\).  Chia sẻ Bình luận
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
|
