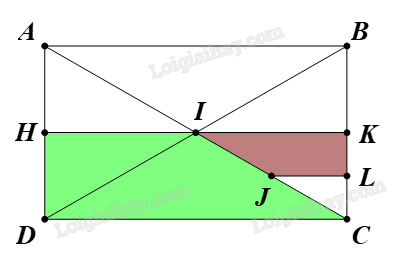
Giải bài 1 trang 40 Chuyên đề học tập Toán 11 Chân trời sáng tạo

Đề bài

Cho hình chữ nhật ABCD có AC cắt BD tại I. Gọi H, K, L và J lần lượt là trung điểm của AD, BC, KC và IC. Chứng minh hình thang JLKI và hình thang IHDC đồng dạng với nhau.

Lời giải chi tiết

Ta có J là trung điểm IC (giả thiết).

Suy ra $\overrightarrow {CI}  = 2\overrightarrow {CJ}$

Do đó ${V_{\left( {C,{\rm{ }}2} \right)}}\left( J \right){\rm{ }} = {\rm{ }}I.$

Chứng minh tương tự, ta được ${V_{\left( {C,{\rm{ }}2} \right)}}\left( L \right){\rm{ }} = {\rm{ }}K,{\rm{ }}{V_{\left( {C,{\rm{ }}2} \right)}}\left( K \right){\rm{ }} = {\rm{ }}B,{\rm{ }}{V_{\left( {C,{\rm{ }}2} \right)}}\left( I \right){\rm{ }} = {\rm{ }}A.$

Vì vậy ${V_{\left( {C,{\rm{ }}2} \right)}}\;$ biến hình thang JLKI thành hình thang IKBA.

Hình chữ nhật ABCD có I là giao điểm của hai đường chéo, suy ra I là trung điểm BD.

Do đó ${Đ_I}\left( B \right){\rm{ }} = {\rm{ }}D.$

Chứng minh tương tự, ta được ${Đ_I}\left( A \right){\rm{ }} = {\rm{ }}C,{\rm{ }}{Đ_I}\left( K \right){\rm{ }} = {\rm{ }}H.$

Lại có ${Đ_I}\left( I \right){\rm{ }} = {\rm{ }}I.$

Do đó Đ_I biến hình thang IKBA thành hình thang IHDC.

Vì vậy phép đồng dạng có được bằng cách thực hiện liên tiếp phép vị tự tâm C, tỉ số 2 và phép đối xứng tâm I biến hình thang JLKI thành hình thang IHDC.

Vậy hình thang JLKI và hình thang IHDC đồng dạng với nhau.